Un vent printanier souffle sur le campus de l’Institut intergalactique et les étudiants en profitent pour lézarder au soleil, dans une atmosphère qui semble propice à l’échange de confidences.
« À quel moment avez-vous su que votre avenir passerait par la mathémagie ? demande Epsilon à ses deux camarades Alpha et Bêta.
‒ J’ai voulu suivre l’exemple de mon grand frère Tau, répond Alpha. Il a intégré l’X n et il faut être un cador en mathémagie pour ça !
‒ Moi, j’aimerais bien que la mathémagie appartienne à mon passé, soupire Bêta. Mais il paraît que ça m’aidera à trouver un travail bien payé, alors… Et toi, Epsilon ?
‒ Je suis tombée un jour sur la formule eiπ + 1 = 0 et j’ai trouvé ça magnifique, confie la jeune fille. J’ai choisi la voie qui me permettrait d’en saisir toutes les subtilités ! »
Bêta s’aperçoit alors que leur conversation est écoutée avec beaucoup d’attention.
« Et vous, Monsieur Phi, qu’est-ce qui vous a poussé à dédier votre vie à la mathémagie ? »
Le professeur se racle la gorge, grommelle quelque peu dans son absence de barbe, mais meurt visiblement d’envie de se départir de sa froideur coutumière pour répondre à son jeune élève.
« Eh bien, se lance-t-il finalement, je crois que tout a commencé le jour où, vers l’âge de 12 ans, je me suis retrouvé enfermé seul dans une pièce vide pendant toute une journée avec pour unique compagnie un lot de boîtes d’allumettes… »
Ignorant le regard effaré de ses étudiants, il poursuit : « Les heures étaient longues et je n’avais rien d’autre à faire à part lancer les allumettes sur le sol et calculer la probabilité qu’elles touchent une rainure du parquet en tombant.
‒ On est d’accord, chuchote Bêta à l’intention de ses camarades, il était déjà atteint avant cet épisode !
‒ Je parvenais à modéliser le problème, continue Phi, faisant mine de n’avoir rien entendu, mais il me manquait des connaissances techniques, comme le calcul d’intégrales, pour arriver à un résultat de manière, disons, classique. »
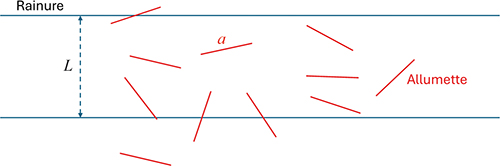
Des allumettes et un calcul de probabilités
En écho à cet épisode vécu plusieurs décennies plus tôt, le professeur Phi trace quelques traits dans le gravier au moyen d’un bâton.
« En réfléchissant, reprend-il, j’ai réalisé plusieurs choses :
1) La probabilité qu’une allumette touche une rainure est égale au nombre d’allumettes lancées qui ont touché une rainure divisé par le nombre N d’allumettes lancées si celui-ci est “très grand” ;
2) Toutes les allumettes lancées mises bout à bout forment un polygone à N côtés qui se rapproche d’un cercle quand N est “grand” – il suffit de les déplacer sans changer leur orientation ;
3) Le problème revient donc à compter le nombre d’intersections de ce cercle avec les rainures du parquet. »
Cher lecteur, avec ces indications, pouvez-vous trouver la probabilité pour une allumette de toucher une rainure en fonction de sa longueur a et de la largeur d’une latte L ?
« Quand on m’a sorti de la pièce, termine le professeur Phi, j’étais subjugué d’avoir rencontré π à un endroit où je ne l’attendais absolument pas ! J’ai trouvé ça…
‒ Mathémagique ! » complète Epsilon avec le sourire complice de ceux qui savent.

