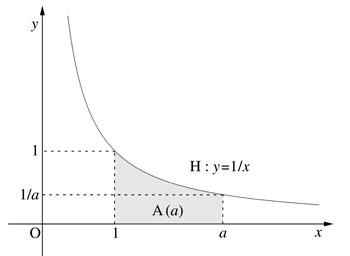
L'importance du problème de la quadrature de l'hyperbole a été affirmée par Marin Mersenne au début du XVIIe siècle. En langage moderne, il s'agit pour l'essentiel de déterminer la mesure de l'aire A(a) que délimitent la courbe H d'équation y = 1/x, l'axe (Ox) des abscisses, la verticale d'abscisse 1 et une autre verticale d'abscisse a quelconque.
Au début du XVIIe siècle, il y a plusieurs bonnes raisons pour s'intéresser à ce problème. La première est que l'hyperbole est l'une des trois « sœurs coniques » (avec l'ellipse et la parabole), qui sont des courbes connues et utilisées depuis l'Antiquité et dont l'intérêt scientifique vient soudain de déborder bien au-delà de la seule géométrie. Quelques années plus tôt en effet, Galilée a découvert que, sur Terre, la trajectoire d'un projectile non soumis à des frottements est une parabole, tandis que Johannes Kepler a proposé de rendre compte du mouvement des planètes à l'aide d'ellipses.
Une autre raison plus mathématique à l'intérêt pour l'hyperbole est que Pierre de Fermat vient de réaliser la quadrature de toutes les courbes de la forme y = xu. En langage moderne, il a trouvé une expression explicite pour une primitive de la fonction f(x) = xu ; ... Lire la suite
