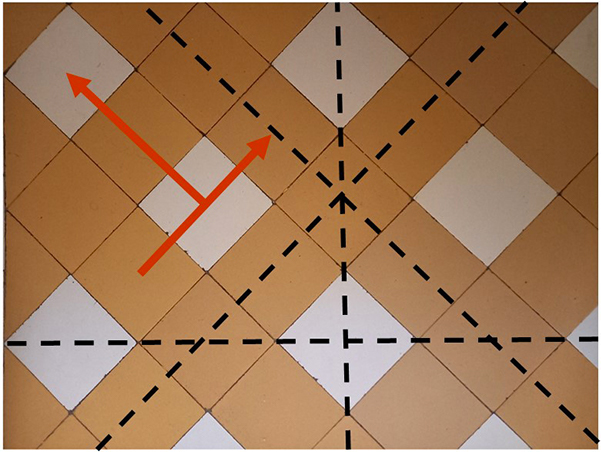
Depuis la plus haute Antiquité, on a cherché à recouvrir de grandes surfaces planes à l’aide de morceaux élémentaires : des pavés pour les routes, des carrelages pour les habitations, des tesselles pour les mosaïques, des motifs pour les textiles, des tuiles pour les toits. Les éléments constitutifs de ces pavages étaient souvent de forme carrée (des carreaux) ou rectangulaire. Leur réalisation en grande quantité était ainsi facilitée et leur juxtaposition régulière, périodique, garantissait un recouvrement plan sans limitation de taille. Une évolution naturelle amena des changements de teintes, de formes et des critères esthétiques pour les motifs reposant sur des notions de symétrie. Les pavages islamiques en sont de magnifiques et nombreux exemples. Heureusement, les mathématiques sont là pour clarifier la situation en classifiant tous les pavages possibles.
Différents types de pavages
Il est intuitif de comprendre le pavage du plan comme son recouvrement par des tuiles jointives sans chevauchement. Demandons de plus que les tuiles aient une « taille minimale » (une aire strictement positive), pour éviter un pavage de type fractal (et une aire limite nulle). Le carrelage de notre salle de bains, et même les pavages plus élaborés du génial Escher répondent bien à cette définition.