La saga des théorèmes : Pythagore
Pythagore est bien plus qu'un mathématicien, dont le théorème, célèbre depuis l'Antiquité, traverse les générations et a suscité à travers les siècles un nombre impressionnant de démonstrations. Qu'on parle avec déférence de l'école pythagoricienne ou avec défiance de la secte des Pythagoriciens, on ne peut oublier que ce personnage mystérieux, dont on ignore presque tout, est au centre d'un édifice philosophique perpétué par ses disciples qui a influencé, au-delà des mathématiques et de l'astronomie, la musique elle-même.

LES ARTICLES
Pythagore bien plus qu'un théorème
Élisabeth Busser
Pythagore, bien plus qu'un célèbre théorème, c'est tout
un édifice philosophique qui va influencer, au-delà des mathématiques et de l'astronomie, la musique elle-même. Au-delà des sciences, l'histoire n'en a donc pas fini avec le « Samien aux longs cheveux » !
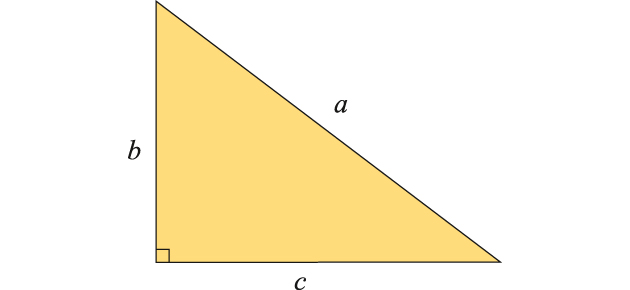
Le théorème de Pythagore est un résultat concernant
des carrés construits sur les côtés d'un triangle rectangle. Les carrés sont ensuite devenus arithmétiques avant que ce théorème ne s'évade vers des espaces abstraits. Pythagore reconnaîtrait-il son théorème s'il ressuscitait
à notre époque ?
Les triplets pythagoriciens
Hervé Lehning
Dans un triangle rectangle, le carré de l'hypoténuse est égal à la somme des carrés des côtés de l'angle droit. Quand cette relation est vérifiée par trois nombres entiers, on parle de triplets pythagoriciens. Qui sont ces nombres, comment les caractériser ?
En bref : Pythagore sans un mot
Fabien AoustinCombien d'élèves sont capables de prouver le théorème de Pythagore ? Ce n'est pourtant pas faute de manquer de démonstrations.
En bref : Et si c'était faux ?
Fabien AoustinLe théorème de Pythagore est-il bien vrai ? La question peut sembler étrange, mais en fait tout dépend du cadre dans lequel on veut appliquer ce résultat de géométrie.
En bref : Le cercle pythagoricien
Patrick Breen et Élisabeth BusserLe rayon du cercle inscrit à un triangle rectangle dont les trois côtés sont entiers est un nombre entier ! Cette petite curiosité arithmétique se démontre très simplement.