D’où vient la topologie ; à quels besoins répond-elle ? Comme pour de nombreux concepts, il n’existe pas de création ex nihilo mais au contraire des approches successives qui rendent incontournable le besoin de faire de notions imprécises une théorie bien construite.
On peut situer les premiers balbutiements avec Gottfried Wilhelm Leibniz, à la fin du XVII e siècle, lorsque le savant et philosophe allemand a souhaité créer une nouvelle géométrie, qu’il nomme analysis situs, différente de celle d’Euclide et de Descartes, qui ne serait pas un « calcul des magnitudes » mais un « calcul des situations ».
En tentant, certes très maladroitement, de définir une notion de limite pour justifier la notion de « différentielle », Leibniz s’est penché sur un autre aspect, que l’on traite désormais par des considérations topologiques. Cette recherche s’est poursuivie avec Jean Le Rond D’Alembert au siècle suivant, puis Augustin Louis Cauchy et Karl Weierstrass dans le courant du XIX e siècle.
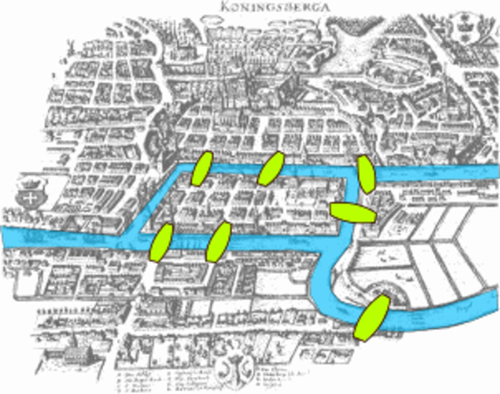
Une approche très différente a été engagée par Leonhard Euler avec son fameux problème des ponts de Königsberg, mais ces considérations restaient certainement pour lui très anecdotiques.