
Parmi les études de Felix Klein figure sa fameuse « bouteille », qui évoque irrésisti-blement un volume que l’on peut remplir. De bouteille il n’en est point car en fait un traducteur allemand s’est à l’origine quelque peu trompé, ou peut-être a voulu faire un jeu de mot, en traduisant Kleinsche Fläche par « bouteille de Klein », au lieu de « surface de Klein » (en allemand, « bouteille » se dit Flasche et surface, Fläche).
L’objet a été décrit pour la première fois en 1882.
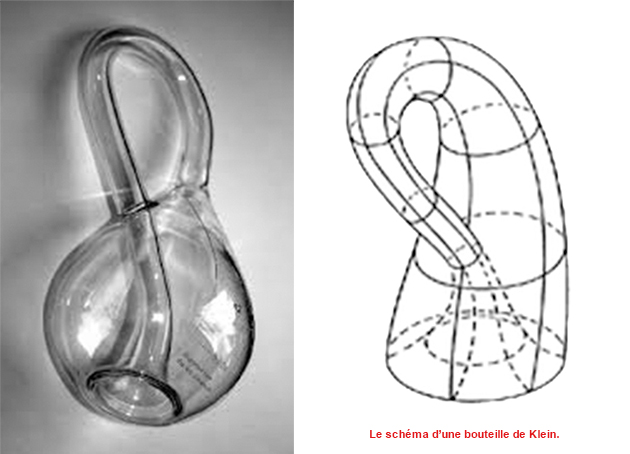
La bouteille de Klein, tout comme l’anneau de Möbius (voir l'article Ceci n'est pas un ruban de Möbius !), est une curiosité topologique. Mais si le ruban de Möbius ne possède qu’une seule face, la fameuse bouteille, quant à elle, est telle qu’aucune distinction n’est possible entre son « intérieur » et son « extérieur ».
La trace du mouvement d’un cercle
Il est maintenant temps de rétablir quelques vérités. Les « surfaces » de Klein peuvent également ressembler à l’illustration suivante, vues dans un espace à trois dimensions.

