
C’est le théorème des quatre couleurs, un fameux résultat de topologie. Si maintenant on tente de colorier le plan P de telle sorte que deux points quelconques distants d’une unité ne soient jamais de la même couleur, combien de couleurs faut-il, au minimum ? C’est le nombre chromatique c (P) du plan. La question a été posée en 1950 par Edward Nelson, mathématicien américain alors étudiant, et publiée par Martin Gardner dans sa chronique du Scientific American. Elle avait déjà été étudiée par le mathématicien suisse Hugo Hadwiger, dont le nom est associé à celui de Nelson pour ce problème. Tous ont transformé le problème à l’aide de graphes dont les sommets figurent les régions du plan et les arêtes le voisinage de ces régions.
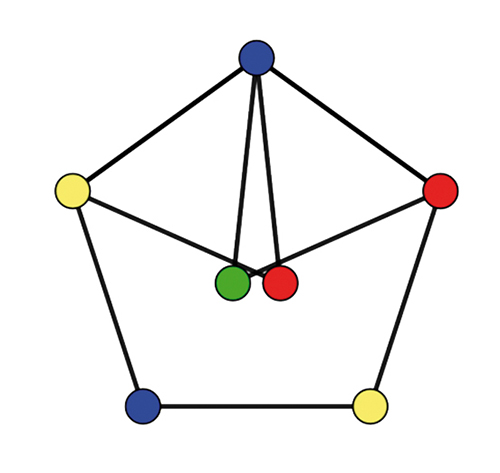
Quatre couleurs sont nécessaires, comme le prouvent les graphes (à sept sommets) des frères Leo et William Moser et celui (à dix sommets) de Solomon Golomb.
La borne supérieure, on la doit au mathématicien américain John Isbell. Il a mis en évidence une solution à sept couleurs : un pavage du plan par des hexagones réguliers de diamètre légèrement inférieur à 1.
C’est d’un mathématicien amateur britannique que vient la dernière avancée. Il vient de publier un article attestant que c (P) ≥ 5. Aubrey de Grey, biologiste de son état, mathématicien à ses heures, rédige en une dizaine de pages ses justifications, faisant intervenir des graphes d’arête 1 mêlés à des fuseaux de Moser pour aboutir à un graphe de 20 245 sommets (!), dont il a testé informatiquement qu’il n’était pas coloriable en quatre couleurs. Depuis, on a simplifié le graphe (on est à 826 sommets), grâce à Marijn Heule, mais on ne sait toujours pas si c (P) = 5, 6 ou 7.
