Les mesures astronomiques de Tycho Brahe (1546–1601), très précises pour l’époque, furent interprétées par Johannes Kepler (1571–1630), qui en induisit ses lois du mouvement des planètes autour du soleil. Pour cela, il utilisa des ellipses, des courbes connues depuis l’Antiquité comme intersection d’un cône et d’un plan.
Des parterres de fleurs dans l’espace
Pour décrire la première loi de Kepler, on exploite une propriété des ellipses, qui par ailleurs les rend faciles à dessiner. Dans un domaine très différent, ce sont les courbes idéales pour former des parterres de fleurs : esthétiques et faciles à construire ! Pour cela, il faut trois piquets et une corde. On plante deux piquets et on y attache la corde, qui doit rester molle. On prend alors l’autre piquet en main et on tend la corde. La courbe décrite par ce piquet mobile quand on tourne autour des deux piquets fixes est une ellipse, dont les foyers sont ces piquets. Un cercle est donc une ellipse dont les deux foyers sont confondus.
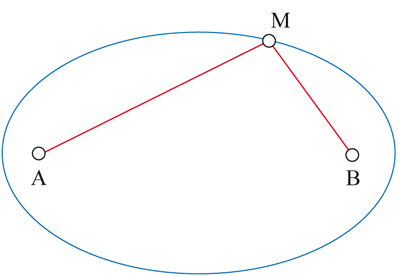
Une ellipse de foyers A et B : ensemble des points M tels que AM + MB est constant.
On peut alors énoncer la première loi de Kepler : les trajectoires des planètes sont ... Lire la suite
