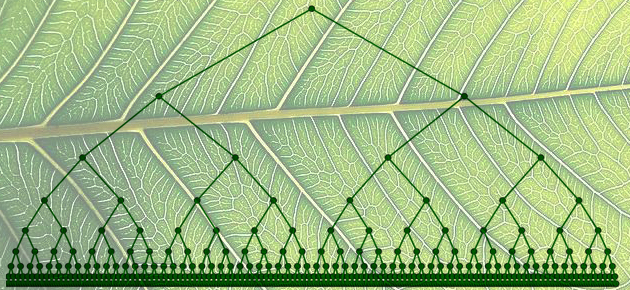
Un arbre binaire complet est une structure combinatoire qui se construit à partir d’un point initial (la racine), duquel partent deux segments (des branches, ou arêtes) qui atteignent deux nouveaux points (des nœuds), desquels partent deux nouveaux segments, et ainsi de suite. Les nœuds successifs sont répartis en lignes, les nœuds de la ligne n étant ceux qui sont rejoints en n segments en partant de la racine. Les nœuds de la dernière ligne, desquels ne partent plus de branches, sont les feuilles de l’arbre.
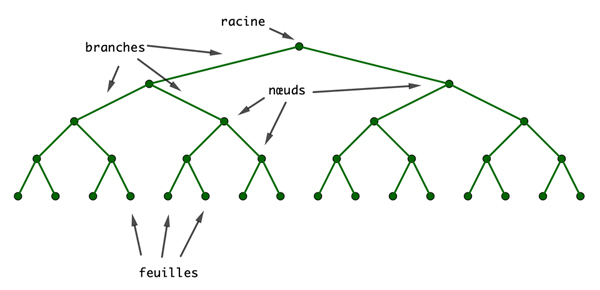
Les notions ainsi définies ressemblent fort à celles qui leur correspondent chez les vrais arbres (ceux en bois), la principale différence formelle étant qu’en combinatoire les arbres ont le plus souvent la racine en haut et les feuilles en bas…
Étiquetons à présent chaque branche selon la marche à suivre pour l’atteindre en partant de la racine, en marquant 0 lorsque l’on va à gauche et 1 lorsque l’on va à droite. On peut interpréter cette étiquette comme l’écriture binaire d’un nombre (voir encadré). En outre, sur le nœud inférieur de chaque arête, écrivons en base 10 la valeur du nombre correspondant. Le nombre 13, par exemple, est l’écriture décimale de « 1101 », qui est l’étiquette de l’arête ainsi atteinte : partant de la racine, on va d’abord ... Lire la suite
