Curieux nombres p-adiques
Au tournant du XX e siècle, l'algébriste Kurt Hensel a eu l'intuition géniale qui a conduit à l'invention des nombres p-adiques. Le système ainsi obtenu a de quoi dérouter : plus besoin de signe « moins », nécessité de développer une nouvelle forme de proximité entre les nombres, apparition d'une topologie étonnante, et surtout… des applications profondes dans tous les domaines des mathématiques !
L'écriture elle-même de ces nombres, différente selon les approches (on peut même les écrire avec des « décimales à gauche »), a de quoi surprendre. Ainsi, on représente un nombre négatif comme –1 à l'aide d'une infinité de chiffres ou comme la somme d'une série qu'on pourrait croire divergente. Une véritable poésie des nombres !
L'écriture elle-même de ces nombres, différente selon les approches (on peut même les écrire avec des « décimales à gauche »), a de quoi surprendre. Ainsi, on représente un nombre négatif comme –1 à l'aide d'une infinité de chiffres ou comme la somme d'une série qu'on pourrait croire divergente. Une véritable poésie des nombres !

LES ARTICLES
Plongée dans un univers numérique étrange
Bertrand Hauchecorne
Au début du xxe siècle, le mathématicien allemand Kurt Hensel « invente » de nouveaux nombres, qui s'écrivent avec une infinité de chiffres, comme dans le système décimal, mais avec une notion de proximité bien différente. Cette curieuse théorie s'est avérée très féconde en arithmétique !
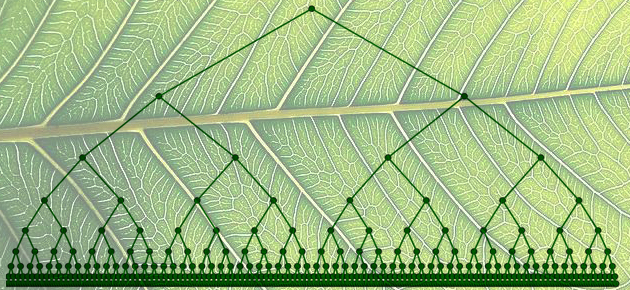
L'arbre dyadique
Benoît Rittaud
Avec un arbre dont les feuilles vont à l'infini, on peut construire, au choix, l'ensemble des nombres entiers positifs ou bien celui des entiers dyadiques. Le truc ? Bien choisir où l'on met les 0 et les 1.
En bref : Kurt Hensel, le père des nombres p-adiques
Bertrand HauchecorneKurt Hensel est principalement connu pour ses travaux sur les nombres p-adiques.