
En créant, à propos de très nombreuses énigmes, des mathématiques accessibles aux amateurs éclairés, John Conway a éclairé d’un jour nouveau et de manière complètement inattendue une grande variété de sujets. Son génie inventif s’est aussi manifesté en géométrie, où il a non seulement imaginé des résultats insoupçonnés, mais créé des jeux et des dispositifs innovants. Il a également revisité à sa manière la démonstration de certains résultats.
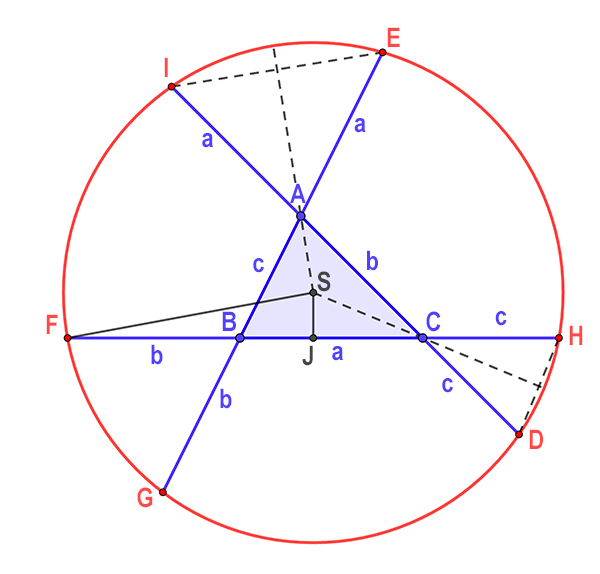
Le cercle de Conway du triangle ABC.
Le cercle de Conway
On part, en toute simplicité, d’un triangle ABC, et on reporte sur les prolongements de ses côtés des longueurs égales à celles des côtés du triangle, ce qui détermine six nouveaux points. Conway a eu l’idée que ces six points sont cocycliques… et il a eu raison ! Le cercle ainsi constitué a évidemment pris le nom de cercle de Conway du triangle ABC.
La preuve de cette cocyclicité tient en peu de mots. Soit S l’intersection des bissectrices du triangle. AI = AE donc (SA) est également médiatrice de [IE] et, par suite, SI = SE. De la même façon, SH = SD et SF = SG. (SA) est également médiatrice de [GD] puisque AG = AD, et (SB) est médiatrice de [EH] puisque BE = ... Lire la suite
