John Conway s’est intéressé aux pavages du plan (voir Découpages et Pavages, Bibliothèque Tangente 64, 2018, pour découvrir certaines de ses contributions majeures). Il a notamment proposé une condition suffisante, mais pas forcément nécessaire, pour qu’un polygone non croisé puisse paver le plan (ce « polygone » pouvant éventuellement être curviligne).
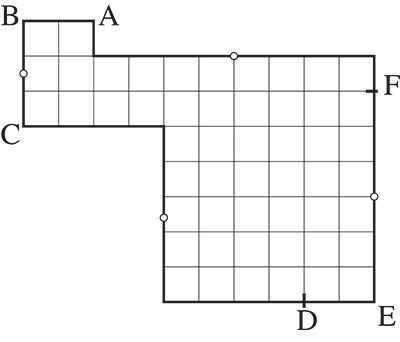
Repérons six points A, B, C, D, E, F, dans cet ordre, sur le pourtour du polygone, tels que :
• les portions [AB] et [DE] du bord soient images l’une de l’autre par une translation ;
• les portions [BC], [CD], [EF] et [FA] du bord possèdent chacune un centre de symétrie (ici [CD] et [FA] ne désignent pas un segment, mais une réunion de segments) ;
• trois au moins des six points A, B, C, D, E, F soient distincts.
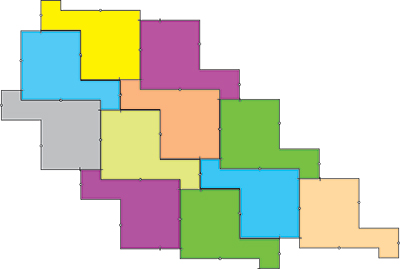
On peut alors réaliser un pavage avec la « brique » ci-dessous, pavage qui ne fait intervenir que des translations et des rotations de 180°.