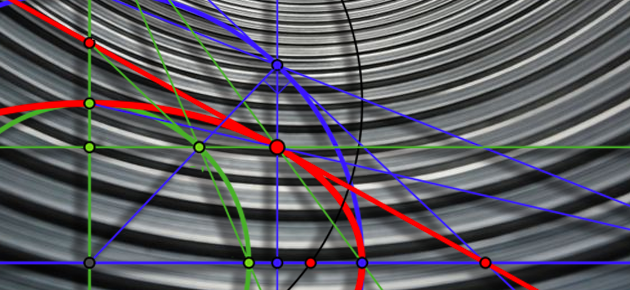
Les coniques figurent parmi les objets géométriques les plus connus. Comment les construire à la règle et au compas ? Commençons avec l’ellipse. Le premier défi est la construction d’un point courant et de sa tangente.
Et plus si affinité…
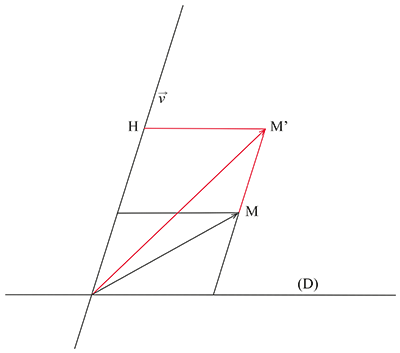
Supposons que l’on connaisse les deux axes d’une ellipse. Pour faciliter le dessin (ce qui n’enlève rien à la généralité de la construction), le grand axe sera ici porté par l’axe des abscisses, le petit axe par celui des ordonnées ; le centre de l’ellipse sera le point O, origine du repère. Le problème est de construire un point courant d’abscisse donnée. On va utiliser le fait que l’ellipse est l’image, par affinité, du grand cercle (et également l’image, par une autre affinité, du petit cercle). Une affinité d’axe la droite (D), de direction le vecteur et de rapport le nombre réel non nul k l’application qui, à tout M du plan, associe le point M’ construit ainsi : par M, on mène la droite de direction
qui coupe (D) en H ; M’ est alors défini par
Lorsque (D) et sont orthogonaux, l’affinité est elle-même qualifiée d’orthogonale.
Le grand ... Lire la suite
