Jésus dit : « Y = aX 2 + bX + c. » Ses disciples de s’interroger : « On ne comprend pas toujours tes paroles, mais là, c’est particulièrement hermétique ! » Et Jésus de répondre : « C’est normal, c’est une parabole. »
La parabole, tout le monde connaît ! Mais on ne sait pas toujours déterminer, à la règle et au compas, le foyer et la directrice d’une parabole, connaissant son axe, un point P et sa tangente ( T ) en P.
Voici un petit guide en cas de situation d’urgence géométrique.
Foyer, doux foyer……
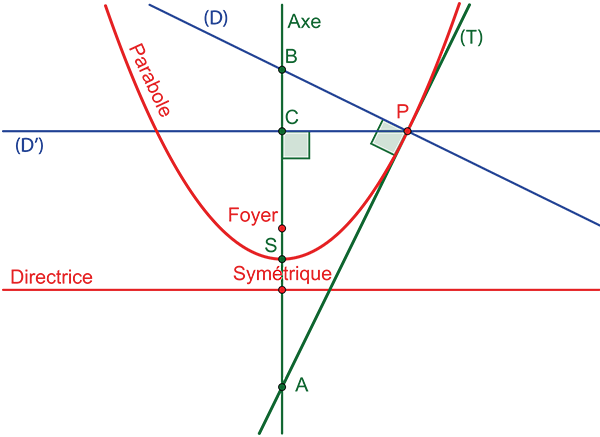
La tangente ( T ) au point P de la parabole coupe l’axe de la parabole au point A.
La perpendiculaire ( D) à la tangente ( T ) passant par le point P coupe l’axe de la parabole au point B ; le foyer de la parabole est alors le milieu du segment [AB].
La perpendiculaire ( D’) à l’axe de la parabole passant par P coupe l’axe en C. Le sommet S de la parabole est le milieu du segment [AC ].
La directrice est la droite perpendiculaire à l’axe de la parabole, passant par le point symétrique du foyer par rapport au sommet S. Ce point se situe sur l’axe de la parabole.