
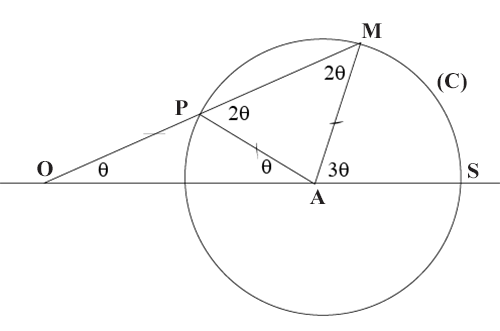
Munissez-vous d’un triangle isocèle AMS. Voulez-vous couper l’angle en trois angles égaux ? C’est facile : tracez le cercle (C) de centre A, passant par S et M, de rayon R = AS = AM. Marquez ensuite sur une réglette deux points O et P distants de R, faites coulisser O sur la droite (AS) et P sur le cercle (C) : lorsque la réglette passe en M, l’angle
trisecte l’angle
.
Regardez bien la figure. Vous trouverez la démonstration en utilisant uniquement le fait que, dans un triangle isocèle, les angles à la base sont égaux, et que la somme des angles d’un triangle vaut 180°.
Cette belle construction a été découverte par les Grecs, grands amateurs de trisection ; c’est en fait la proposition VIII du Livre des lemmes dans les Œuvres complètes d’Archimède. Mais bien que les instruments utilisés soient la règle et le compas, ceci n’est pas une construction « à la règle et au compas » car les points O et P ne sont pas construits par tracés successifs de cercles et de droites.
Faisons maintenant varier l’angle θ, les points A et O restant fixes : le point M décrit alors une certaine ... Lire la suite
