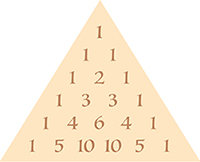
Au XVIIe siècle, Pierre de Fermat introduit le procédé de « descente infinie », bien mal dénommé puisque, précisément, la « descente » est finie. Le raisonnement par récurrence, quant à lui, pourrait être qualifié de « montée à l’infini » (voir En Bref « Pierre de Fermat, un célèbre contemporain »). À la même époque, Pascal crée un outil remarquable qui s’y apparente. Étrangement, il ne l’utilisera que rarement dans ses écrits mathématiques, préférant souvent démontrer « par l’exemple » et jugeant inutile d’expliciter la montée vers l’infini. Ce défaut de rigueur est-il propre à Pascal ? Non, les mathématiciens, aux XVIIe et XVIIIe siècles, se contentent souvent de « démontrer par l’exemple », quand l’intuition le permet, comme s’il existait des « idées claires et distinctes » (comme l’écrit Descartes) que l’on n’avait pas à analyser plus que nécessaire mais seulement à faire sentir aux lecteurs. Le XIXe siècle montrera les limites de ces pratiques et apportera aux mathématiques beaucoup plus de rigueur.