Un triangle avec trois côtés entiers ? Voilà qui n’a rien de sensationnel. Si d’aventure il vous prenait l’envie d’exiger que le triangle soit aussi rectangle, pour apporter un peu de fantaisie, il serait possible de vous décrire toutes les possibilités qui s’offrent alors à vous ; c’est le fameux problème de la recherche des triangles pythagoriciens (voir Tangente 212, 2023). Mais quittons les triangles et explorons le monde des quadrilatères.
Des quadrilatères entiers
En trouver un dont tous les côtés sont entiers est aussi trivial que pour les triangles : prenez par exemple un carré de côté 1. Exigeons maintenant que les diagonales aussi soient des nombres entiers. Le carré de côté 1, avec ses diagonales de longueur ne convient plus.
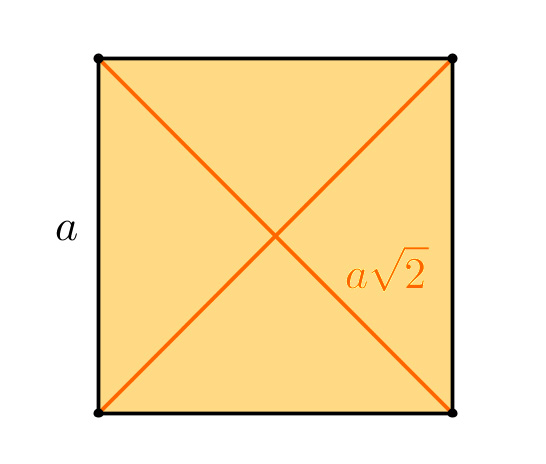
Pour le carré, si les côtés sont entiers, les diagonales ne le sont pas.
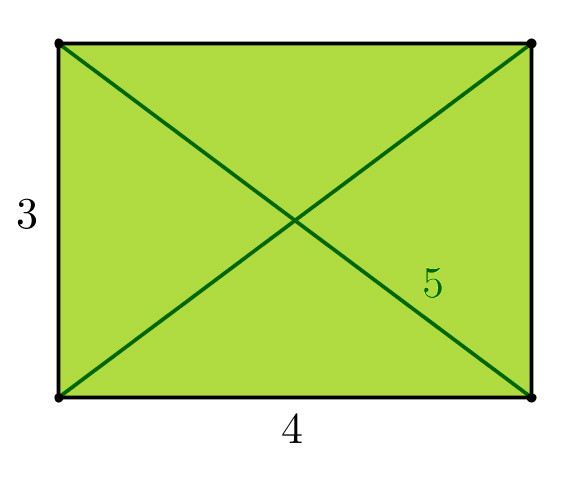
Le rectangle de côtés 3 et 4 et de diagonale 5 peut nous satisfaire. Il en est de même de tout rectangle dont les côtés sont les deux nombres les plus petits intervenant dans un triangle pythagoricien.