Professeur non titulaire de l’université de Zurich, Albert Einstein accepte en 1910 un poste à Prague, ville alors allemande. L’un de ses plus proches collègues à l’université est le mathématicien austro-hongrois Georg Pick. Ce dernier l’aurait, selon certains, initié à la géométrie différentielle, car, au cœur du très flegmatique Pick, cohabitait le même intérêt pour la théorie et la pédagogie.

Georg Pick (1859-1942).
Mais Pick est surtout connu pour avoir établi, en 1899, un théorème sur l’aire d’un polygone qui accepte plusieurs démonstrations élémentaires, illustrant ainsi la notion de « beauté » en mathématique.
Le plus de l’additivité
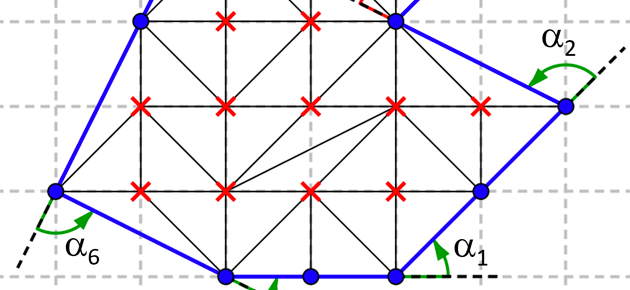
Considérons un polygone P dont les sommets sont sur les intersections d’un réseau régulier de maille unité. On nomme I le nombre de points du maillage intérieurs à ce polygone et B le nombre de ceux, sommets compris, qui appartiennent à sa frontière (le bord). On peut raisonnablement penser qu’une formule de l’aire S d’un tel polygone, si elle existe, ne dépend que de ses caractéristiques B et I.
Commençons par montrer la notion fondamentale d’extensivité d’une surface, à savoir que la surface de deux domaines d’intersection nulle est égale à la somme des ... Lire la suite
