
Un triangle est entièrement déterminé, à une symétrie près, par la longueur de ses côtés. Mais quelle est son aire ? Pour répondre à cette question, on dispose, depuis environ deux millénaires, de la formule de Héron, mathématicien et astucieux ingénieur originaire d’Alexandrie. L’aire S d’un triangle de côtés a, b et c est donnée par où p est le demi-périmètre du triangle.
Après trois, quatre
Jouons maintenant avec les quadrilatères en prenant le cas particulier d’un quadrilatère dont les longueurs des côtés sont, dans l’ordre, 6, 8, 10 et 12. On sait qu’un tel objet n’est pas unique et donc que son aire n’est pas complètement déterminée. Mais ajouter une diagonale de longueur donnée rigidifie le quadrilatère et fixe alors son aire, qu’on calcule en appliquant la formule de Héron aux deux triangles ainsi définis.
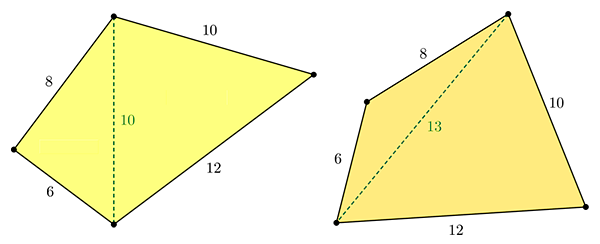
Selon la formule de Héron, l’aire du quadrilatère de gauche vaut 72,
et l’aire de celui de droite vaut environ 73,7.
À défaut, quelle est, pour quatre côtés donnés, la plus grande aire possible pour un quadrilatère ? On montre qu’elle est obtenue pour des quadrilatères inscriptibles dans un cercle, dits cycliques par la suite. Notons ... Lire la suite
