Entrer les mots « Pascal triangle » dans le cartouche de recherche de l’Encyclopédie de Neil Sloane et Simon Plouffe fournit plus de deux mille résultats. La première réponse (A007318) concatène la rangée zéro (le « 1 » tout en haut du triangle), puis la rangée 1 (composée de deux « 1 »), puis la rangée 2 (les entiers « 1 », « 2 » et « 1 »), puis la rangée 3 (« 1 », « 3 », « 3 », « 1 »)… On obtient la suite S = 1, 1, 1, 1, 2, 1, 1, 3, 3, 1, 1, 4, 6, 4, 1, 1, 5, 10, 10, 5, 1, 1, 6, 15, 20, 15, 6, 1, 1, 7, 21, 35, 35, 21…

Trois éléments suffisent pour construire un triangle du même aloi : ce sont les entiers qui composent le « côté gauche » du triangle (uniquement des « 1 » chez Pascal), les entiers qui composent le « côté droit » (idem) et une règle permettant de calculer les termes « intérieurs » (la règle est, chez Pascal, que la somme de deux entiers voisins est écrite pile en dessous).

La suite A029635 remplace tous les « 1 » du côté droit du triangle par des « 2 » et concatène à son tour les rangées obtenues. Ce triangle, reformaté sous forme de rectangle, porte parfois le nom de tableau de Viète. La suite A074909 remplace les « 1 » du côté droit par la suite des entiers naturels non nuls. Le triangle obtenu est celui de Pascal, amputé de son côté droit.

La suite A199512 se base sur un triangle dont le côté gauche est la suite de Fibonacci et le côté droit la suite de Fibonacci purgée des termes de rang pair. Comme pour tous les triangles précédents, un terme intérieur est la somme des deux qui le surmontent – mais l’intérêt supplémentaire vient ici de ce que chaque terme intérieur (ainsi que chaque terme du côté gauche) est aussi la différence entre son voisin de droite immédiat et le terme qui surmonte la paire. Ainsi 144 (en bas à droite) est-il la somme de 55 et 89 mais aussi (par construction) la différence entre 233 et 89 :

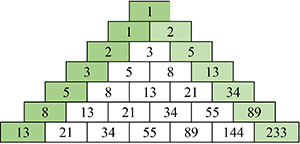
À vous de jouer et d’expérimenter !

Voici deux triangles « à la Pascal » qui ne sont pas dans l’Encyclopédie. Le premier a pour sommet zéro, puis pour côté droit les nombres premiers et pour côté gauche les nombres composés. Il ne tient qu’à vous d’en trouver les propriétés et de les soumettre à l’OEIS !

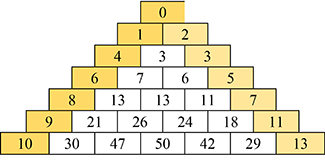
La suite associée au triangle ci-dessus (toujours selon la technique de la « concaténation par rangées successives ») est T = 0, 1, 2, 4, 3, 3, 6, 7, 6, 5, 8, 13, 13, 11, 7, 9, 21, 26, 24, 18, 11, 10, 30, 47, 50, 42, 29, 13… Présente-t-elle des particularités mathématiques ? Comment varie par exemple la proportion de termes premiers de T par rapport aux entiers composés ?

Le triangle suivant (formé d’entiers bleus) semble très artificiel : il dépend de la base 10. On demande que tous ses termes contiennent le chiffre « 1 ».

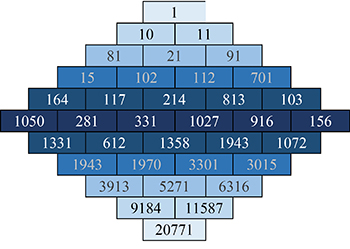
Les termes ci-dessus ne sont probablement pas les plus petits possibles contenant le chiffre « 1 » mais ils illustrent une « construction en diamant » : tout nouveau terme provoque une cascade de résultats qui doivent obéir à la règle. Ainsi « 1050 » (à gauche du diamant), ajouté à son voisin « 281 », donne-t-il bien « 1 331 ». Ce sera aussi le cas, mécaniquement, de tous les autres termes sur la même diagonale descendante.

À vous de faire preuve de créativité en imposant vos propres règles de construction et en explorant le résultat ! Si vous trouvez d’intéressantes propriétés mathématiques, n’oubliez pas de les soumettre à l’OEIS…