Que nous inspire la suite ci-dessous, en dehors de son aspect semblant à première vue imprévisible ?

(A) : 0, 0, 0, 0, 1, 0, 2, 1, 2, 1, 4, 1, 5, 2, 3, 3, 7, 2, 8, 3, 5, 4, 10, 3, 9, 5, 8, 5, 13, 3, 14, 7, 9, 7, 11, 5, 17, 8, 11, 7, 19, 5, 20, 9, 11, 10, 22, 7, 20, 9, 15, 11, 25, 8, 19, 11, 17, 13, 28, 7, 29, 14, 17, 15, 23, 9, 32, 15, 21, 11, 34, 11, 35, 17, 19, 17, 29, ...

On peut déjà observer la suite des premières occurrences de chacun des entiers représentés en bleu : 0, 1, 2, 4, 5, 3, 7, 8, 10, 9, 13, 14, 11, 17, 19, 20, 22, 15, 25, 28, 29, 23, 32, 34, 35...

Les rangs de ces nombres dans la suite initiale sont les suivants :

(B) : 1, 5, 7, 11, 13, 15, 17, 19, 23, 25, 29, 31, 35, 37, 41, 43, 45, 47, 51, 53, 59, 61, 65, 67, 71, 73, 75...

Il ne vous échappera pas que beaucoup de ces nombres sont des nombres premiers, mais pas tous : ce n’est pas le cas de 1, 15, 25, 35, 45, 51, 65, 75, par exemple. 

La suite (B) contient tous les nombres premiers ainsi que des nombres impairs composés. On peut s’intéresser à la forme de ces derniers. Nous n’avons pas la réponse ici.

Où intervient l’indicateur d’Euler 

La suite ci-après correspond à l’indicateur d’Euler des entiers non nuls. Pour chaque entier positif non nul, elle indique le nombre d’entiers positifs strictement inférieurs à n  et premiers avec n.

(C ) : 1, 1, 2, 2, 4, 2, 6, 4, 6, 4, 10, 4, 12, 6, 8, 8, 16, 6, 18, 8, 12, 10, 22, 8, 20, 12, 18, 12, 28, 8, 30, 16, 20, 16, 24, 12, 36, 18, 24, 16, 40, 12, 42, 20, 24, 22, 46, 16, 42, 20, 32, 24, 52, 18, 40, 24, 36, 28, 58, 16, 60, 30, 36, 32, 48, 20, 66, 32, 44, ...

En ôtant 1 à chacun de ces nombres et en prenant la partie entière de la moitié du résultat, on retrouve... la suite (A). La suite (A) donne en fait, pour chaque entier n, le nombre d’entiers strictement compris entre 1 et n/2 et premiers avec n.

Il est à noter que, même en allant assez loin (par exemple, sur les 10 000 premiers termes de (A) ; voir sur oeis.org la suite A055684), on ne rencontre aucun multiple de 6. Est-ce vrai pour la suite toute entière ? La question reste ouverte. D’autres nombres semblent également absents de cette suite…

Quel rapport avec les polygones ? 

Chaque valeur a(n) de la suite (A) donne le nombre de polygones réguliers étoilés différents ayant n sommets et n côtés. La première valeur de n pour laquelle il existe un polygone étoilé à n côtés est n = 5.

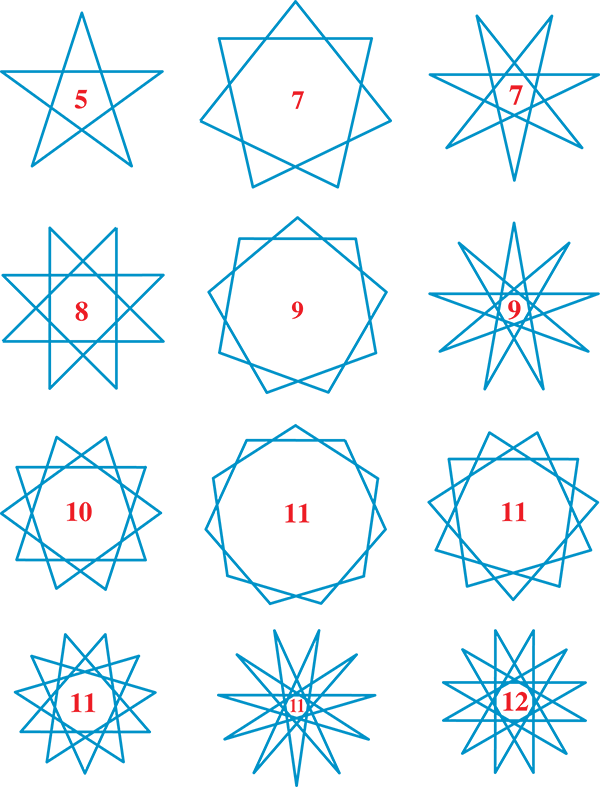
Il n’existe pas de polygone étoilé à 3 ou 4 côtés. 

On en trouve un seul à 5 côtés : le pentagramme, le seul nombre p tel que 1 < p < 5/2 étant 2. Il suffit de relier les sommets d’un pentagone régulier de 2 en 2 (voir ici).

Il n’y a pas d’hexagone étoilé, l’hexagramme, constitué de deux triangles équilatéraux superposés n’étant pas un polygone à proprement parler.

Il existe deux heptagones réguliers étoilés : on peut relier les sommets de 2 en 2 ou de 3 en 3.

Un seul octogone régulier étoilé peut être obtenu – en reliant les sommets de 3 en 3 –, l’octogramme constitué de deux carrés superposés n’étant pas un vrai polygone.

On trouve deux ennéagones réguliers étoilés, un seul décagone étoilé, quatre hendécagones étoilés, un seul dodécagone étoilé...