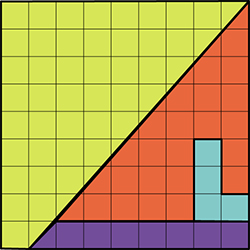
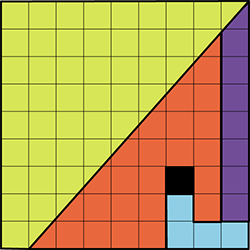
En 1953, Paul Curry, un magicien amateur de New York, présenta le puzzle paradoxal suivant, désormais connu sous le nom de triangle de Curry.
Les deux « triangles », représentés sur un quadrillage régulier à mailles carrées, sont composés d'un assemblage des mêmes pièces : un triangle jaune d'aire 12 carreaux, un triangle violet d'aire 5 carreaux et deux gnomons d'aires 8 carreaux (en vert) et 7 carreaux (en bleu). Dans la disposition de droite, un carreau blanc supplémentaire est apparu. D'où vient-il ?
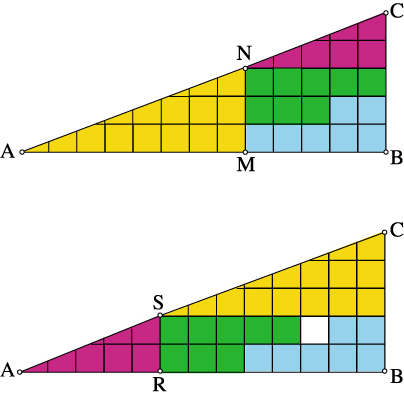
Les deux figures rappellent la configuration basique du théorème de Thalès. Calculons donc les rapports AM / AB et MN / BC d'une part, et AR / AB et RS / BC d'autre part (l'unité étant le côté d'un petit carré du quadrillage). On constate que : et que
.
La conclusion du théorème de Thalès (égalité des rapports) n'est donc pas vérifiée. Que peut-on en conclure ? En appliquant la contraposée du théorème de Thalès, on peut dire que l'une (au moins) des prémisses du théorème est fausse. Mais laquelle ?
Si le quadrillage est régulier, les droites (MN) et (BC) sont bien parallèles, de même que (RS) et (BC).
Les points M et R sont bien supposés être des points de la droite (AB). Mais les points N et S sont-ils des points de la droite (AC) ? C'est là que le bât blesse ! Les points A, N et C semblent alignés, de même que les points A, S et C. Mais ils ne le sont pas… Enfin, pas tout-à-fait. De telle sorte que l'œil ne distingue pas le léger décalage, vers l'intérieur du triangle pour une des figures, et vers l'extérieur pour l'autre.
En effet, l'aire du triangle ABC devrait être de 32,5 carreaux unités. Or elle ne compte que 32 carreaux unités dans une des figures (celle de gauche) et elle compte 33 carreaux unités dans l'autre (celle de droite).
Vous trouverez maintenant sans peine le « défaut » permettant d'ajouter un carreau dans le puzzle suivant, créé par Gianni Sarcone et Marie-Jo Waeber ( archimedes-lab.org/ ).
