Comme nous le montre notre dossier « Pythagore », le nom de ce grand mathématicien, s'il évoque d'abord la géométrie, est aussi familier des théoriciens des nombres. On sait tout, ou presque, sur les triplets pythagoriciens. Mais que peut-on dire des triplets « presque » pythagoriciens ?

Un triplet presque pythagoricien est un triplet d'entiers positifs (x, y, z) tels que x² + y² = z² ± 1. Déjà, on connaît des solutions de l'équation x² + y² = z² + 1 ; on sait même en générer une infinité à partir des triplets pythagoriciens (voir l'article d'Eunmi Choi), mais on ne sait pas générer toutes les solutions. Les tableaux ci-après donnent quelques « petites » solutions.

Dans le tableau de gauche, les triangles obtenus sont tous « presque » rectangles, mais aussi « presque » isocèles, la « presque » hypoténuse et un côté de l'angle « presque » droit différant d'exactement une unité. Dans le tableau de droite, on remarque le triangle isocèle « presque » rectangle (5 ; 5 ; 7).

On connaît également des solutions de l'équation x² + y² = z² – 1. Le tableau ci-après en propose plusieurs.

Des triangles sur une planche à clous 

Sur une planche à clous, des clous sont disposés aux sommets d'un quadrillage à mailles carrées (on le supposera de dimensions aussi grandes qu'on le souhaite). Il est facile de réaliser un triangle rectangle à côtés entiers (l'unité étant le côté d'une maille du quadrillage) en plaçant tout simplement un élastique autour de trois clous. Le triangle ABC en fournit un premier exemple, à savoir le triangle (3 ; 4 ; 5). Le triangle DEF, c'est-à-dire (5 ;12 ; 13), constitue un autre exemple.

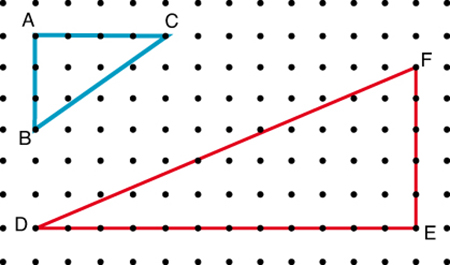
1. Mais est-il possible de former sur la planche à clous un triangle rectangle à côtés entiers dont aucun côté ne soit horizontal ni vertical ?

Revenons maintenant aux triangles « presque » rectangles.

2. Est-il possible de former sur la planche à clous un triangle presque rectangle à côtés entiers ?

3. Même question pour un triangle presque rectangle dont les côtés ont pour longueurs des nombres réels. Il s'agit ici de trouver trois sommets du quadrillage tels que les trois longueurs des côtés du triangle formé par ces trois sommets soient des solutions réelles de l'équation x² + y² = z² ± 1.