
Le paradoxe suivant fut présenté par Martin Gardner dans l’une de ses chroniques du magazine Scientific American. Il avait été proposé au ludologue américain par A. Kenneth Austin, de l’université de Sheffield en Angleterre. Il donnera lieu à de nombreux courriers de lecteurs, certains contestant les conclusions, voire l’absence de conclusion nette et définitive apportée à ce problème.
Albert et Zoé partent au même instant d’un point A pour se rendre à un point B distant de 6 km. Lui avance à une vitesse constante de 6 km/h tandis que Zoé ne marche qu’à une vitesse constante de 4 km/h. Ils sont accompagnés de leur chien Mirza qui, depuis le départ et pendant tout le trajet, fait la navette entre son maître et sa maîtresse à la vitesse constante de 10 km/h. On suppose que ses demi-tours successifs se font instantanément. On pose alors la question suivante : où se trouve précisément le chien Mirza exactement une heure après son départ ?
Où est donc passé Mirza ?
Curieusement, il est impossible de répondre avec précision à cette question. Ou plutôt, il existe une infinité de réponses possibles, le chien pouvant se trouver une heure après son départ en n’importe quel point de l’intervalle [AB] situé à 2 km ou moins de 2 km de B !
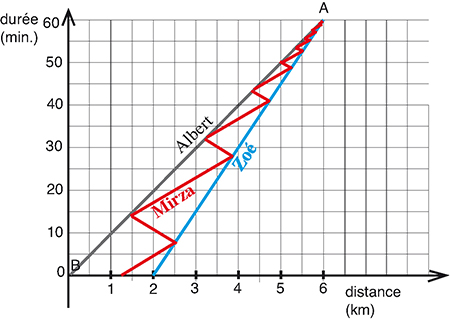
En effet, supposons qu’après exactement une heure Albert soit parvenu en B, alors que Zoé est encore à deux kilomètres de B, qu’ils décident, en se téléphonant, de faire demi-tour et de repartir vers A, en conservant leurs vitesses respectives, et que leur chien continue ses allers-retours entre ses deux maîtres, toujours à la vitesse de 10 km/h. Si l’on attribue l’abscisse 0 à B et l’abscisse 6 à A, quel que soit le point de l’intervalle [0, 2] d’où repart le chien, au bout d’une heure, il arrivera en même temps que ses maîtres en A, en ayant parcouru exactement 10 km.
1. Quel est le rapport entre les longueurs de deux trajets successifs du chien vers sa maîtresse (ou vers son maître) ?
Le paradoxe est dû au fait que dans le retour illustré ici le trajet du chien se termine par une infinité d’allers-retours, mais que les distances parcourues convergent (comme les distances dans le paradoxe de la flèche de Zénon qui, en parcourant la moitié de la distance entre sa position de départ et la cible, puis la moitié du reste, etc., finit pourtant par atteindre sa cible). À l’aller, le mouvement du chien au départ est impossible à décrire précisément, d’autant plus que le passage instantané d’une vitesse de 10 km/h dans un sens à la même vitesse dans le sens opposé suppose une décélération, puis une accélération, infinies.
Pire encore : on trouve une situation analogue, sans discontinuité dans la direction et le sens, avec le problème suivant. Un ULM part d’un point de l’équateur, et se dirige à vitesse constante et à altitude constante selon une direction Est–Nord-Est sur une loxodromie (une courbe qui coupe tous les méridiens rencontrés sous un même angle). On supposera que l’angle, constant, avec le Nord est de 45°. Cette route finit par s’enrouler autour du pôle Nord selon une spirale logarithmique.
Supposons que notre ULM revienne ensuite selon une direction Sud–Sud-Ouest. Reviendra-t-il à son point de départ sur l’équateur ? La réponse est que l’ULM peut, au retour, arriver en n’importe quel point de l’équateur, puisqu’en partant du pôle Nord il existe une infinité de façons de se diriger vers le Sud–Sud-Ouest. La longueur L d’une telle route est donnée par L = π (R / 2) cos (45°), où R est le rayon du globe terrestre.
2. Quelle serait la distance parcourue par l’ULM entre l’équateur et le pôle Nord ?

