Cet arboretum possède de magnifiques spécimens provenant du monde entier. Les neuf plus beaux sont disposés en losanges. Le conservateur vient de constater que les racines de l’arbre A sont attaquées par une bactérie particulièrement virulente, ce qui le condamne malheureusement à dépérir puis à mourir. Cette maladie se transmet de proche en proche par les racines, chaque arbre malade ne pouvant la transmettre qu’aux plus proches. Par ailleurs, les spécialistes savent que les arbres ont exactement une chance sur deux d’être naturellement résistants à la maladie et donc de ne pas êtres infectés.

1. Quelle est la probabilité pour que l’arbre B, supposé non résistant à la maladie, finisse par être infecté ?

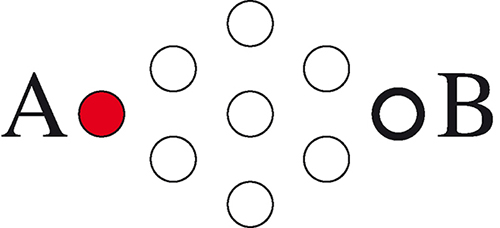
Pour que la maladie n’atteigne pas l’arbre B, il faut et il suffit qu’il existe un « barrage d’arbres résistants » bloquant la progression de la maladie vers l’arbre B. Un tel barrage reliera deux côtés du losange.

Cette situation n’est pas sans rappeler le jeu de Hex, où deux joueurs s’affrontent pour créer un chemin reliant deux bords opposés d’un tableau en forme de losange, le but étant de créer un chemin formé de pions d’une seule couleur reliant les deux bords de cette couleur.

Hex a été co-inventé par le physicien danois Piet Hein (1905–1996) et le mathématicien américain John Nash (1928–2015). Il ne peut y avoir de partie nulle : on finit obligatoirement par former soit un chemin reliant les deux bords blancs (Blanc gagne), soit un chemin reliant les deux bords noirs (Noir gagne).

Et maintenant, percolons…

Supposons maintenant que le plateau du jeu de Hex, entièrement recouvert de pions blancs et noirs, représente un agrégat non homogène de roches dont certaines sont poreuses (les bords blancs et les pions blancs) et d’autres imperméables (les bords noirs et les pions noirs). Un fluide pourra-t-il traverser ce milieu ? La réponse est positive si Blanc gagne, et négative s’il existe un chemin de pions noirs reliant les deux bords noirs et « faisant barrage ». Dans la pratique, c’est évidemment plus complexe, car il faut prendre en compte la viscosité du fluide, la pression qu’il subit, la perméabilité plus ou moins importante du matériau poreux…

Mais ce plateau pourrait aussi représenter un milieu non homogène dont certains éléments sont conducteurs de l’électricité (les bords et les pions blancs) et d’autres résistants (les bords et les pions noirs). Dans un cas, le courant passe entre les deux bords blancs, et dans l’autre, il ne passe pas.

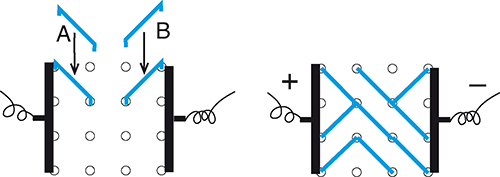
On dispose de deux électrodes métalliques entre lesquelles se trouve un réseau à mailles carrées de trois petits carrés sur trois. Pour chaque petit carré élémentaire de ce réseau, on peut enficher une barette conductrice sur une des diagonales (les deux positions possibles sont illustrées en A et B.

On enfiche neuf barettes (une par petit carré), en choisissant à chaque fois au hasard une des deux diagonales (cf. la figure de droite, où le courant passe de l’électrode de gauche à celle de droite). On applique ensuite une tension électrique aux bornes des deux électrodes.

2. Quelle est la probabilité pour que le courant passe ?