Quand la science nourrit l'art : Escher et Poincaré

Le graveur néerlandais Maurits Escher est bien connu des passionnés de mathématiques. Cet artiste était en effet curieux de toutes les possibilités qu’offre la géométrie, qu’elle soit « classique », c’est-à-dire euclidienne, ou non, et de ses possibles paradoxes lorsque l’on veut représenter une situation en trois dimensions sur une feuille de papier… qui n’en a que deux.

Maurits Cornelis Escher (1898-1972).

Escher a eu des contacts avec de nombreux mathématiciens de son temps. En 1954, il a rencontré le mathématicien britannique Roger Penrose (voir Tangente 198, 2021) et a ensuite repris l’idée de son escalier paradoxal dans une de ses œuvres. La même année (le Congrès international des mathématiciens se déroulait à Amsterdam), il a aussi rencontré le Canadien Donald Coxeter, à qui il a demandé comment représenter sur papier, dans un espace fini, l’idée d’un univers infini. Coxeter lui a alors suggéré d’utiliser le principe du disque de Poincaré et de la géométrie hyperbolique. Il a résulté de cet échange une série d’œuvres d’Escher, intitulées Limite circulaire I, II, III et IV.

Une géométrie non euclidienne

Le disque de Poincaré est un objet topologique ouvert : le bord, qui n’appartient pas au disque, symbolise des points situés à l’infini. Sur ce disque, la mesure de la longueur dépend de l’éloignement au centre.

Les « droites » de cet univers, c’est-à-dire les chemins de plus courte distance d’un point à un autre – on parle alors de géodésiques –, sont les diamètres du disque et tous les arcs de cercle dont les extrémités sont perpendiculaires aux bords. La géométrie de ce disque est dite non euclidienne, car l’axiome des parallèles d’Euclide n’y est pas vérifié. En effet, par un point donné, il passe une infinité de droites parallèles – de droites non sécantes - à une droite donnée.

Le travail d’Escher a consisté à créer des pavages périodiques sur le disque de Poincaré, les éléments du pavage se reproduisant à l’infini lorsqu’on s’approche du bord du disque.

1. Comment tracer une géodésique ?

Sur le disque de Poincaré, la somme des angles d’un triangle n’est pas égale à 180°, mais est toujours strictement inférieure à 180°.

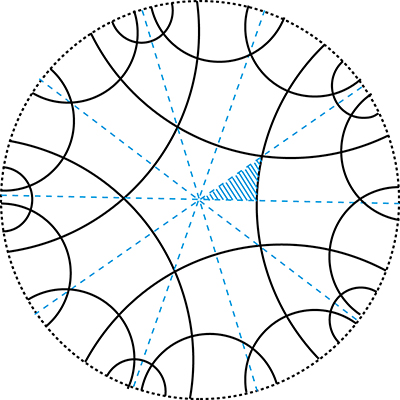
Considérons un pavage du disque de Poincaré par des pentagones réguliers (au sens de la géométrie hyperbolique). Les angles de ces pentagones sont tous des angles droits ! Chaque pentagone peut être décomposé en dix petits triangles hyperboliques, comme illustré pour le pentagone central sur la figure qui représente les premières étapes de la construction du pavage pentagonal.

2. Quelles sont les mesures des trois angles du triangle hachuré de la figure ?

Une belle formule permet de calculer l’aire d’un triangle hyperbolique (pour la métrique associée à cette géométrie). Cette formule est due au mathématicien Jean-Henri Lambert (1728-1777), qui avait établi la formule analogue dans le cas de la géométrie sphérique.

L’aire A d’un triangle en géométrie hyperbolique est donnée par la relation , où  et   sont les mesures en radians des angles du triangle et où k est une constante qui dépend de l’unité utilisée.

3. Déterminez l’aire du triangle hachuré de la figure en prenant k = 1.