L’expérience proposée ici met en évidence certaines propriétés des angles d’un polygone quelconque, qu’il soit croisé ou non, en n’effectuant quasiment aucun calcul. Mais n’attrapez pas le tournis…
On place une allumette en A1 sur le côté [A1A2] de l’hexagone croisé A1A2B1A3B2B3. On fait ensuite glisser cette allumette sur le côté [A1A2] jusqu’à ce qu’elle bute en A2. On la fait alors pivoter dans le sens trigonométrique, la tête restant sur le sommet A2, et on la met en contact avec le côté [A2B1]. On la fait glisser le long de ce côté pour amener son extrémité en B1. On la fait pivoter à nouveau, autour de B1, cette fois-ci dans le sens horaire, pour l’amener en contact avec le côté [B1A3]. On continue ainsi, la rotation se faisant dans le sens trigonométrique pour les angles en A1, A2 et A3, et dans le sens horaire pour les angles en B1, B2 et B3, jusqu’à faire revenir l’allumette dans sa position de départ.
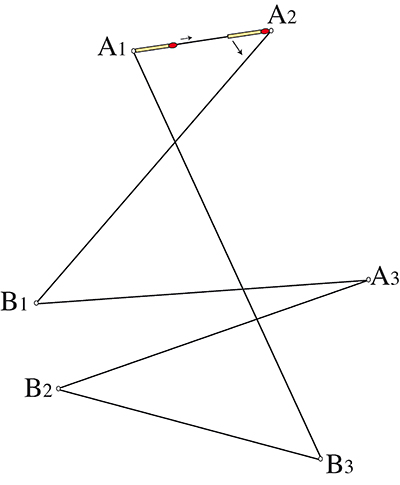
Entre sa position initiale et sa position finale, de quel angle l’allumette a-t-elle tourné ? On se convainc facilement qu’elle n’a fait aucun tour, en remarquant par exemple qu’elle n’a jamais été orientée selon un axe Nord-Sud, mais qu’elle a en quelque sorte « oscillé » autour d’un axe Ouest-Est.
On en déduit que la somme des angles saillants en A1, A2 et A3 est égale à la somme des angles saillants en B1, B2 et B3.
Arrondissons les angles
Refaisons cette expérience, mais en ajoutant une contrainte. On suppose maintenant que la ligne polygonale fermée A1A2B1A3B2B3 est un mur infranchissable et que l’allumette est placée à l’intérieur de l’angle saillant en A1. On procède ensuite comme dans l’expérience précédente, sauf que lorsque l’allumette arrive en B1, B2 et B3, ne pouvant franchir un mur, elle est obligée de tourner dans le sens antihoraire en décrivant les angles rentrants.
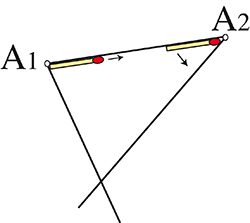
Une fois revenue dans sa position de départ, de quel angle l’allumette aura-t-elle tourné au cours de son périple ? Munis d’une allumette, d’un crayon et d’une feuille de papier, on peut vérifier qu’elle aura fait trois tours. En effet, le somme des angles que l’allumette aura décrits est égale (en degrés) à
soit
Or par le raisonnement précédent ; on a donc bien effectué trois tours.
Pourtant, la somme des angles intérieurs d’un polygone simple (non croisé) est égale à
(n – 2)×180°, soit par exemple 720° ou deux tours pour un hexagone.
Considérons maintenant notre hexagone comme constitué de tiges rigides articulées et décroisons-le. On aboutit à l’hexagone A1A2B’1A3B’2B3.
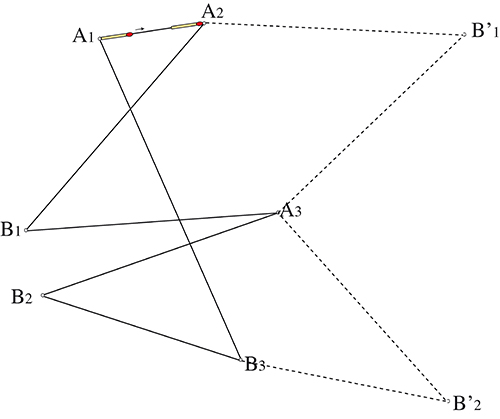
Montrez que l’on retrouve bien deux tours pour la somme des angles intérieurs de ce polygone et que l’on a « gagné un tour » en dépliant le polygone.

