Dans l’ensemble ℕ des nombres entiers naturels, l’équation ab = a + b ne possède que deux solutions : 0 + 0 = 0 × 0 = 0 et 2 + 2 = 2 × 2 = 4.
L’équation a + b + c = abc, quant à elle, n’en possède qu’une seule non triviale : 6 = 3 + 2 + 1 = 3 × 2 × 1.
Par ailleurs, tout nombre entier non premier supérieur ou égal à 6 peut être écrit sous ces deux formes égales suivantes, à condition d’utiliser suffisamment de termes (ou de facteurs) égaux à 1 ; par exemple :
8 = 2 + 2 + 2 + 1 + 1 = 2 × 2 × 2 × 1 ;
24 = 4 + 3 + 2 + 1 + 1 +… + 1 = 4 × 3 × 2 × 1 (avec quinze « 1 ») ;
2 024 = 23 + 11 + 8 + 1 + 1 +… + 1 = 23 × 11 × 8 × 1 (avec mille neuf cent quatre-vingt-deux « 1 »).
1. Écrivez 2 024 d’une manière similaire en utilisant le plus petit nombre de termes possible.
Et avec des carrés ?

Norman Peter Herzberg (1937–2020).

Adolf Hurwitz (1859‒1919).
Le problème suivant a été étudié en 1907 par le mathématicien allemand Adolf Hurwitz : quelles sont les solutions dans ℕ des équations du type x12 + x22 +… + xn2 = k × x1 × x2 ×… × xn, en dehors des solutions triviales où x1 = x2 =… = xn = 0, et x1 = x2 =… = xn = 1 avec k = n ?
Listons quelques exemples où k = 1 pour de petites valeurs :
16 = 22 + 22 + 22 + 22 = 2 × 2 × 2 × 2 ;
24 = 32 + 22 + 22 + 22 + 12 + 12 + 12 = 3 × 2 × 2 × 2 × 1 × 1 × 1 ;
27 = 32 + 32 + 32 = 3 × 3 × 3 ;
36 = 42 + 32 + 32 + 12 + 12 = 4 × 3 × 3 × 1 × 1.
D’autres solutions existent avec une valeur de k supérieure à 1 :
8 = 22 + 12 + 12 + 12 + 12 = 4 (2 × 1 × 1 × 1 × 1 ) ;
10 = 22 + 12 + 12 + 12 + 12 + 12 + 12 = 5 (2 × 1 × 1 × 1 × 1 × 1 × 1) ;
12 = 22 + 22 + 12 + 12 + 12 + 12 = 3 (2 × 2 × 1 × 1 × 1 × 1).
Le mathématicien américain Norman Herzberg reprit cette exploration dans un article de 1972.
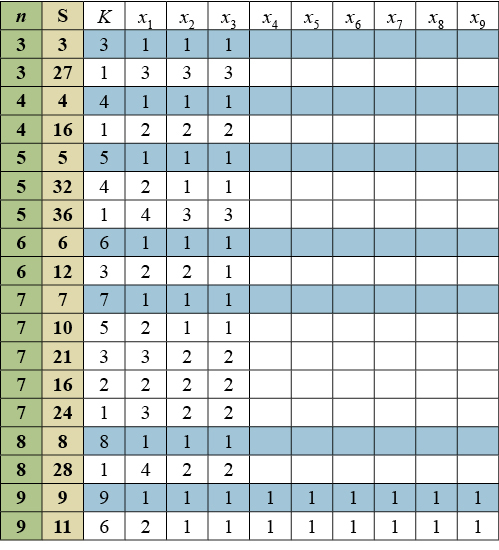
Ce tableau donné par Hurwitz sera prolongé par Herzbergjusqu’à n = 45.
S désigne la somme des carrés des xi ; les solutions triviales apparaissent en bleu.
Curieusement, il existe des valeurs de n pour lesquelles les seules solutions sont triviales : 12, 24, 32, 48, 60, 108, 240, 384, 480, 608, 972, 984, 1 020, 2 688. Elles sont toutes congrues à 0 ou à 8 modulo 12. On n’en connaît pas d’autres jusqu’à 108, et on conjecture que ce sont les seules.
2. Écrivez 2 024 comme une somme de carrés de nombres entiers naturels égale au produit de ces mêmes entiers naturels.
SOURCES
• Über eine Aufgabe der unbestimmten Analysis. Adolf Hurwitz, Archiv der Mathematik und Physik III, 1907. • On a problem of Hurwitz. Norman Herzberg, Pacific Journal of Mathematics 50 (2), 1974.

