L'échiquier de Neper

Avec la méthode exposée par Neper dans son ouvrage Rabdologiae, un échiquier de taille habituelle (huit cases sur huit) permet d'effectuer des calculs jusqu'à 2⁸ – 1, c'est-à-dire jusqu'à 255, mais on peut bien sûr utiliser un damier de plus grande taille pour aller au-delà.

Le principe de l'addition est très simple. Il se ramène à effectuer le calcul en base 2. On décompose les nombres à additionner en base 2, et on place des jetons dans les colonnes correspondant au chiffre 1, celles correspondant au chiffre 0 restant vides.

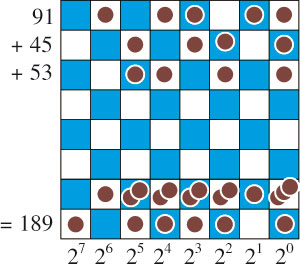
Prenons l'exemple de l'addition 91 + 45 + 53. Le nombre 91 se décompose en 2⁶ + 2⁴ + 2³ + 2¹ + 2⁰ (ce qui correspond à l'écriture binaire 1011011) ; on place donc un jeton dans les 1^re, 2^e, 4^e, 5^e et 7^e colonnes à partir de la droite. On procède de même pour 45 et 53.

On regroupe ensuite les jetons, colonne par colonne, sur l'avant-dernière ligne par exemple. Puis on applique le principe des retenues de droite à gauche, de façon à ne jamais laisser plus d'un seul jeton par case (dernière ligne). Pour ce faire, lorsqu'une case contient plus d'un jeton, on remplace deux jetons par un seul jeton que l'on place dans la case située immédiatement à gauche ; on itère cette opération jusqu'à ce que chaque case contienne au plus un jeton (dernière ligne de l'échiquier). On obtient alors l'écriture en base 2 du résultat de l'addition.

Les soustractions peuvent se faire d'une façon tout à fait similaire. Lorsqu'on ne peut soustraire, on « emprunte » un jeton dans la case immédiatement à gauche en le doublant.

Le gain de temps n'est pas évident, mais il faut voir qu'au XVI^e siècle la majorité de la population était illettrée et ne maîtrisait aucune technique de calcul…

Les multiplications aussi

Pour les multiplications, l'échiquier de Neper devient nettement plus performant, s'adressant là encore à un public n'ayant aucune connaissance des tables de multiplication.

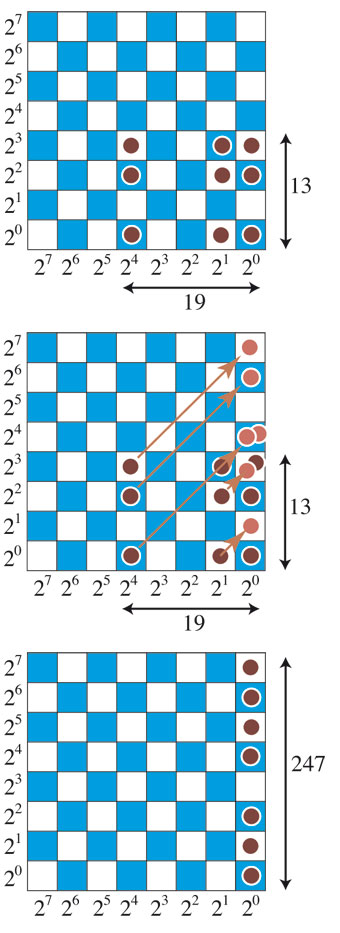
On place le multiplicande sur l'axe horizontal, sur la rangée du bas de l'échiquier, et le multiplicateur sur l'axe vertical, dans la colonne de droite. Les jetons du multiplicande sont répétés sur chaque ligne correspondant à un 1 du multiplicateur écrit en base 2, les lignes correspondant à un 0 restant vides.
Ensuite, on déplace tous les jetons selon une diagonale montante, de façon à placer tous les jetons dans la dernière colonne. Il reste enfin à supprimer les jetons multiples en remplaçant systématiquement deux jetons par un seul jeton placé dans la case immédiatement supérieure, jusqu'à ce que toutes les cases de la dernière colonne contiennent au plus un seul jeton. On obtient alors la décomposition en base 2 du résultat. Il reste à additionner les puissances de 2 correspondant aux seules cases contenant un jeton.

En utilisant l'échiquier de Neper, multipliez 15 par 17. 

L'échiquier de Neper permettait aussi, d'après son auteur, de faire des divisions ainsi que l'extraction de racines carrées, mais l'explication des procédures à utiliser devient nettement plus sophistiquée…