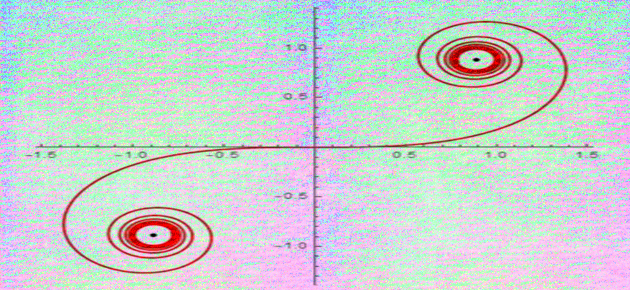
Une courbe paramétrée est définie par la position d’un point M(t) de la courbe en fonction d’un paramètre, souvent noté t car, historiquement, c’était le temps. Les coordonnées (x,y) du point M sont donc fonction de t : on peut écrire x = f (t) et y = g (t), où f et g sont des fonctions numériques. Selon les cas, elles sont continues, de classe C1 (les dérivées existent et sont continues), de classe C n (les dérivées existent et sont continues jusqu’à l’ordre n), de classe C∞ (les dérivées existent pour tous les ordres et sont donc continues) …
Si l’on veut éviter les courbes trop « pathologiques », comme celles de Peano et de Lebesgue (voir article « Donner une définition précise ? Pas si simple ! »), on ne s’intéressera qu’aux cas où f et g sont au moins de classe C1 sur leurs domaines de définition. Dans la pratique, la classe C2 suffit, en général, pour étudier la courbe de manière satisfaisante, qu’il s’agisse du comportement local (tangente, centre et rayon de courbure, point d’inflexion…) ou de son aspect global (variations, branches infinies, convexité…). Voyons un cas particulier important. Lorsque l’on se donne une fonction f de variable réelle et à valeurs réelles, ... Lire la suite
