
Après l’« invention » par René Descartes, dans son ouvrage fondamental Géométrie (1637), de la géométrie analytique, avec l’introduction des coordonnées, et les travaux de Pierre de Fermat à la même époque, les mathématiciens ont étudié de manière systématique les courbes définies par une équation du type P(x, y) = 0, où P est un polynôme en deux variables. Dénommées courbesgéométriques par Descartes, elles sont appelées maintenant courbesalgébriques. Par exemple, la courbe algébrique donnée par l’équation x 2 + 2 y 2 − 2 x − 2 = 0 est une ellipse. Celle définie par y 2 (1 + x) = x 2 (1 − x) est une cubique particulière : c’est une strophoïde. On y voit un point double. La courbe d’équation (x 2 + y 2 − 1)3 − x 2 y 3 = 0 est une sextique : c’est le cœur de Beutel. On y devine deux points de rebroussement.
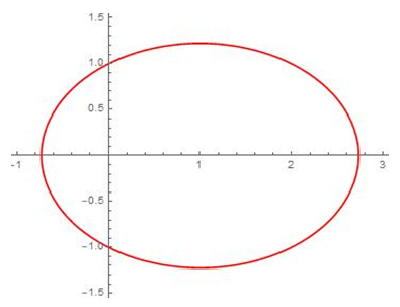
Une ellipse.
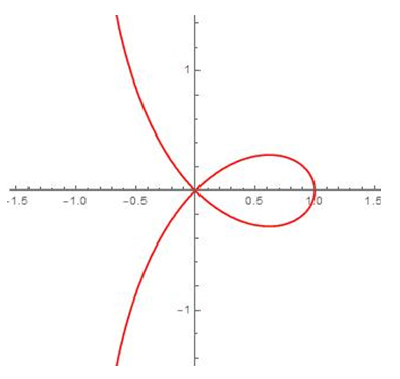
Une strophoïde.
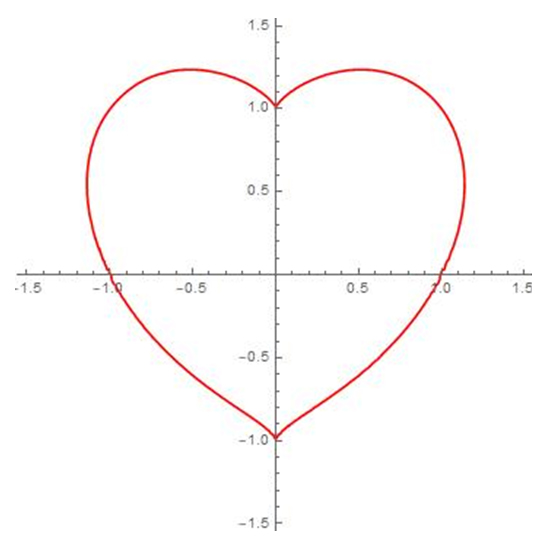
Le cœur de Beutel.
Quand les degrés montent…
Les courbes algébriques sont classées selon le degré du polynôme P. Or, si l’on élève P au carré, l’équation correspondante produit la même courbe que celle définie par P (x, y) = 0, mais le degré n’est alors plus le même ! De manière générale, on supposera que le polynôme P ne contient pas de facteur carré. Dans ce cas, ... Lire la suite
