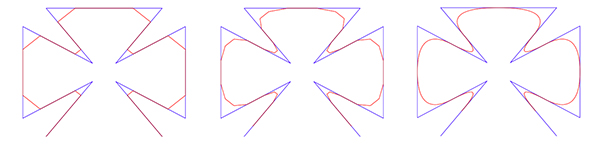
Une parabole à partir de trois points
Partons de trois points P0, P, et P2. On applique l’algorithme suivant, qui comprend deux étapes :
On note Q 0 et Q 1 les milieux des deux segments [ P0P1 ] et [ P1P2 ] ;
On note R le milieu du segment [ Q 0Q 1 ].
En sortie, on obtient un point R et deux suites de trois points, P0, Q 0, R et R, Q 1, P2, sur lesquelles on peut réitérer l’algorithme.
.jpg)
Tous les points construits de cette manière appartiennent à une parabole (qui passe donc par P0, R et P1). Le polygone P0P1P2 est appelé polygone de contrôle de la parabole.
Cet algorithme, consistant uniquement à tracer des segments et à en déterminer le milieu, est aisé à mettre en œuvre (avec une règle et un compas, ou tout logiciel de géométrie dynamique). Il est également adapté aux processus de compression puisque l’on peut lui adjoindre un critère d’arrêt qui dépend de la résolution voulue.
Augmenter le degré
L’algorithme de de Casteljau - car c’est de lui qu’il s’agit - utilisé pour générer une parabole (voir ci-dessous) peut être légèrement modifié, en ajoutant une étape, de manière à pouvoir être appliqué à un polygone à quatre sommets. On engendre alors une cubique.
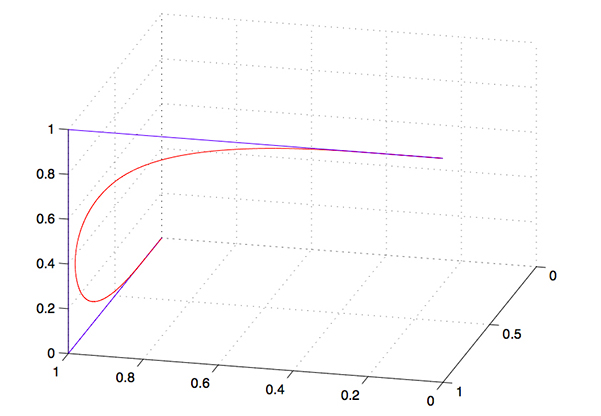
Lorsque les quatre sommets du polygone ne sont pas coplanaires, la cubique ne l’est pas non plus ; on a alors affaire à une courbe gauche.

Un polygone de contrôle à n sommets dont trois successifs ne sont pas alignés va engendrer une courbe de degré n.
En coupant les coins
Un autre algorithme de génération de courbes, dû à George Chaikin, consiste à « couper les coins » (c’est le processus corner-cutting) à partir d’un polygone de contrôle. Le polygone obtenu à chaque étape est alors « de plus en plus proche » de la courbe limite. En raccourcissant chaque côté du polygone de contrôle d’un quart de sa longueur à ses deux extrémités, et en réitérant le processus, la courbe limite est une courbe spline de degré 2, c’est-à-dire une courbe composée d’arcs de paraboles raccordés de manière C 1.