
Comment passe-t-on de la simple définition où le nombre π est le rapport entre le périmètre du cercle et son diamètre à la danse de ses décimales ? La réponse va dépendre de l’époque où on se pose la question !
Tout élève de primaire qui a dessiné une rosace sait que, pour obtenir un hexagone, il suffit sur un cercle de reporter son rayon R. Cette simple observation est peut-être à l’origine du goût de certains pour la géométrie.
De là, on déduit que le périmètre est « un peu plus grand » que six fois le rayon, soit une première valeur de π, à savoir 3, avec zéro décimale.
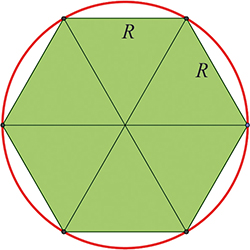
Au début, avec la géométrie
Cette constatation, les Babyloniens l’avaient déjà faite dans une tablette cunéiforme de plus de 4000 ans ! Ils avaient même obtenu bien mieux (voir en page 10)
en évaluant la valeur de π à (dans la suite de cet article, les décimales incorrectes seront en rouge).
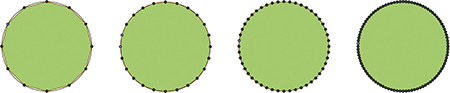
Polygones à douze, vingt-quatre, quarante-huit et quatre-vingt-seize côtés.
Les Égyptiens, eux, dans le fameux papyrus de Rhind, utilisent un octogone irrégulier et arrivent à l’approximation soit 3,16.
Le progrès remarquable de ... Lire la suite
