
Une situation extrêmement importante pour définir des courbes est celle donnée par un champ de vecteurs. Dans le plan, il s’agit d’attacher à chaque point une flèche, que l’on interprète comme une vitesse. Ce dernier mot est ici pris dans son sens physique : une vitesse possède une direction, un sens, et une intensité (cette dernière étant proportionnelle à la longueur de la flèche). On peut alors se figurer un champ de vecteur comme correspondant, en chaque point, à la vitesse de l’eau d’une rivière qui s’écoule sans variation dans le temps.
Une approximation de la trajectoire

Champ de vecteurs modélisant l’écoulement d’une rivière.
Un bouchon déposé à la surface de cette rivière va alors suivre la trajectoire que lui impose le champ de vecteurs. Une question naturelle consiste à déterminer, le champ étant fixé ainsi que la position initiale B0 du bouchon, ce que sera cette trajectoire.
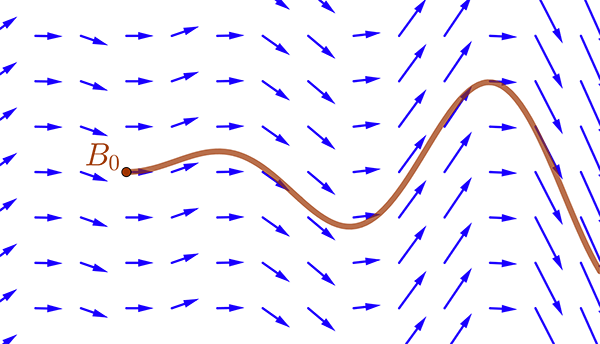
Trajectoire réelle du bouchon.
Bien souvent, à la fois pour des raisons physiques et mathématiques, le champ de vecteurs est supposé continu, c’est-à-dire que les flèches de deux points voisins sont toujours elles-mêmes de direction et de taille voisines. Malheureusement, même avec ... Lire la suite
