Au XVIIe siècle, Pierre de Fermat introduit le procédé de « descente infinie », bien mal dénommé puisque, précisément, la « descente » est finie. Le raisonnement par récurrence, quant à lui, pourrait être qualifié de « montée à l’infini » (voir En Bref « Pierre de Fermat, un célèbre contemporain »). À la même époque, Pascal crée un outil remarquable qui s’y apparente. Étrangement, il ne l’utilisera que rarement dans ses écrits mathématiques, préférant souvent démontrer « par l’exemple » et jugeant inutile d’expliciter la montée vers l’infini. Ce défaut de rigueur est-il propre à Pascal ? Non, les mathématiciens, aux XVIIe et XVIIIe siècles, se contentent souvent de « démontrer par l’exemple », quand l’intuition le permet, comme s’il existait des « idées claires et distinctes » (comme l’écrit Descartes) que l’on n’avait pas à analyser plus que nécessaire mais seulement à faire sentir aux lecteurs. Le XIXe siècle montrera les limites de ces pratiques et apportera aux mathématiques beaucoup plus de rigueur.
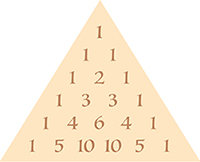
Le triangle de Pascal (voir article « Les propriétés du triangle arithmétique »).
Les cellules constituant les deux bords du triangle qui se rejoignent au sommet sont constituées uniquement de chiffres 1. L’entier qui figure dans toute cellule
(par exemple 6) est la somme des entiers qui se trouvent dans les deux cellules du dessus (3 + 3). Le nombre situé dans la « colonne » p (oblique, contenant un élément de chaque ligne en comptant à partir de 0) et la ligne n (en comptant à partir de 0 les lignes) indique le nombre de combinaisons possibles de p éléments dans un ensemble à n éléments et vaut donc , noté encore 
, soit !}.)
L’origine du raisonnement par récurrence
Le raisonnement par induction consiste, à partir d’une collecte d’observations, à formuler une loi générale ; ce raisonnement est omniprésent dans les sciences de la nature. Le raisonnement par déduction consiste, à partir d’une loi, à en tirer des conséquences, en utilisant le raisonnement logique. L’induction va du particulier au général, la déduction du général au particulier.
En mathématiques, l’induction n’a pas sa place, en principe, puisque la spécificité des mathématiques est de démontrer des résultats généraux en se fondant sur quelques principes admis, les axiomes. Pourtant, au XVIIe siècle, les mathématiciens utilisent le raisonnement par induction, ou plutôt la « preuve par l’exemple » : en donnant quelques exemples signifiants, ils en déduisent des énoncés généraux.
On sait combien l’intuition est trompeuse en mathématiques : Descartes commit quelques « erreurs », Fermat a formulé des conjectures restées célèbres qui se révélèrent erronées (sans toutefois prétendre qu’elles étaient vraies). Même Euler et Cantor ont été trompés par l’intuition ! Pascal, lui, semble ne s’être jamais trompé, bien qu’utilisant fréquemment la « preuve par l’exemple » : il refusa de se confronter à des problèmes où l’intuition pouvait le tromper, par exemple en théorie des nombres.
Le raisonnement par récurrence permet, avec toute la rigueur nécessaire, de passer du particulier au général ; on évoque encore l’induction mathématique ou l’induction complète.
Un exemple classique de raisonnement par récurrence
Calculons, en fonction de l’entier naturel n, la somme 1 + 2 + 3 +… + n. Notons Sn cette somme, définie pour n supérieur à 1. Par un artifice classique, on devine que Sn = n (n + 1)/2. Il suffit par exemple de remarquer que 2Sn est égal à :
(1 + 2 + 3 + … + n) + (n + (n – 1) + (n – 2) + … + 1), et donc à (1 + n) + (2 + (n – 1)) +… + (n + 1), soit encore à n (n + 1).
L’égalité Sn = n (n + 1)/2 semble prouvée pour tout n. Elle est par exemple vraie pour n = 1 ou pour n = 2. Le raisonnement par récurrence est alors utilisé pour confirmer ce que l’intuition laisse supposer.
• La formule Sn = n (n + 1)/2 est vraie pour n = 1. Supposons-la vraie pour un entier n et calculons Sn+1. Cette dernière somme vaut Sn + (n + 1), soit n (n + 1)/2 + (n + 1), soit encore (n + 1)(n / 2 + 1), que l’on peut écrire (n + 1)(n + 2) / 2, qui est bien le résultat espéré.
• Par le principe de récurrence, le résultat est démontré pour tout entier naturel n supérieur à 1.
Un exemple moins intuitif
Dans certains cas, la « formule à deviner » est beaucoup plus subtile ; Pascal s’est confronté aux combinaisons et a avoué avoir procédé par l’expérience et avoir rencontré beaucoup de difficultés.
Calculons par exemple le nombre Pn de permutations de n objets. Si n = 1, il y a, bien sûr, une seule permutation. Si n = 2, il y en a deux. Peut-on en conclure que pour n = 3 il existe trois permutations ? Non : si l’on désigne par A, B, C les trois objets distincts à permuter, on voit qu’il y a trois choix possibles pour l’objet associé à A, puis seulement deux choix possibles pour l’objet associé à B et, finalement, un seul choix possible pour l’objet associé à C. L’idée est alors de poser Pn = n! (où la factorielle de n est définie par n! = 1 × 2 × 3 × … × n).
On a P1 = 1!, puis P2 = 2! et aussi P3 = 3!. Calculons Pn+1. Les n+1 objets à permuter sont notés A1, A2…An+1. On fixe l’objet associé à A1. Soit Ak l’objet associé à A1. Il y a n! manières d’associer les n objets A2, A3… An+1 aux n objets A1… Ak‒1, Ak+1… An+1. Comme il y a (n + 1) choix possibles pour Ak, on en déduit bien que Pn+1 = (n+1) × n! = (n + 1)!. Ici, le raisonnement par récurrence s’impose pour se convaincre du résultat.
D’autres précurseurs
Dans la lettre de M. Amos Dettonville (un pseudonyme) à M. de Carcavy, écrite dans les années 1657‒1658, Pascal cite explicitement un prédécesseur : « Cela est aisé par Maurolic et de là paraît la vérité de ma proposition. » Il invoque Maurolic (1494‒1575), aussi appelé François Maurolyc par Marin Mersenne, ou même Marulle par Étienne Pascal, pour justifier l’affirmation suivante : « Tout nombre triangulaire pris deux fois et diminué de son exposant est le même que le carré de son exposant. » Le nombre triangulaire Tn d’exposant n est 1 + 2 +… + n, soit n (n + 1) / 2. Il est évident (d’après l’encadré ci-dessus) que 2Tn ‒ n = n2.
Suivant William Henry Bussey dans son article de 1917 The Origin of Mathematical Induction, citant lui-même l’article Maurolycus, the First Discoverer of the Principle of Mathematical Induction signé par Giovanni Enrico Eugenio Vacca en 1909, il apparaît que Maurolycus a largement participé à la diffusion en Europe des œuvres d’Euclide, d’Archimède, ou encore d’Apollonius, et il a écrit l’ouvrage Arithmeticorum libri duo dans l’année 1557 (publié en 1575). C’est à cette occasion qu’il utilise un raisonnement par récurrence. Il démontre, par exemple, que n2 + (2n + 1) = (n + 1)2 et en déduit que 1 + 3 + 5 + … + (2n + 1) = (n + 1)2 pour tout n.
Il procède en général de la manière suivante pour démontrer qu’une propriété P (n) est vraie pour tout entier n : il montre P (1), P (2), P (3), P (4), P (5) et conclut par une simple phrase que le résultat général s’en déduit pour n = 6, puis n = 7, etc. Ce n’est donc pas un véritable raisonnement par récurrence, tout comme Pascal procèdera plus tard (en raisonnant à partir d’exemples).
Trois occurrences chez Pascal
Pascal est considéré, selon la tradition, comme l’inventeur du raisonnement par récurrence. Il l’utilise dans ses démonstrations au moins à trois reprises : dans la conséquence 12 de son Traité du Triangle arithmétique (voir article « Les propriétés du triangle arithmétique »), pour établir la règle des partis (voir article « L'art du partage équitable »), et lorsqu’il fait usage du triangle arithmétique pour les combinaisons. Regardons ce dernier raisonnement.
La proposition 1 [lemme V] du Traité du Triangle arithmétique s’énonce ainsi : « En tout Triangle arithmétique, la somme des cellules d’un rang parallèle quelconque égale la multitude des combinaisons de l’exposant du rang dans l’exposant du Triangle. »
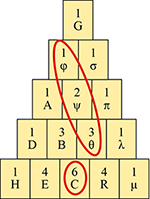
Illustration de la propriété énoncée par Pascal : la somme des trois nombres entourés se lit directement dans le tableau.
Reformulons ce passage. Le mathématicien considère le triangle GDλ. Il affirme en fait, simplement, que la somme des cellules consécutives prises dans une diagonale quelconque peut se lire directement dans le triangle de Pascal. Par exemple, la somme φ + ψ + θ (qui se trouve sur la deuxième diagonale du triangle de Pascal) est égale au nombre de combinaisons du nombre 2 (qui est le numéro de cette diagonale, comptée à partir du bord du triangle) dans le nombre 4 (qui est le numéro de la ligne où termine la diagonale). Or ce nombre (ici, 6) est localisé de manière non ambiguë dans le triangle de Pascal !
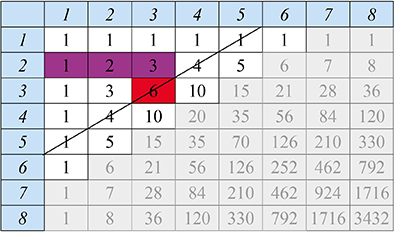
On peut aussi représenter le triangle de Pascal sous la forme d’un tableau rectangulaire dans lequel la lecture se fait selon les diagonales montantes
(par exemple, la cinquième ligne du triangle de Pascal « traditionnel »
se lit ici le long de la diagonale qui relie les deux « 6 » en italique).
Blaise Pascal indique que la somme des cellules violettes
est égale à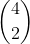 
(en rouge).
Si l’exposant du triangle est 1, la proposition est évidente.
Examinons comment procède ensuite Pascal. Le lemme second est ainsi formulé : « S’il se trouve un Triangle arithmétique dans lequel cette proposition se rencontre, c’est-à-dire dans lequel, quelque rang que l’on prenne, il arrive que la somme des cellules soit égale à la multitude des combinaisons de l’exposant du rang dans l’exposant du triangle : je dis que le triangle suivant aura la même propriété. »
Pascal démontre le second lemme en se fondant sur un exemple, en choisissant un triangle « quelconque », le troisième ; il montre que, pour chaque rang parallèle, la propriété est vraie, puis il considère le quatrième triangle et le second rang parallèle ; la propriété est encore vérifiée ; il conclut : « On le montrera de même de tous les autres. »
Ainsi, Pascal ne démontre pas vraiment la proposition par récurrence, mais procède à la manière de Maurolycus : il suppose P (1) ; il montre, sur un exemple, que si P (n) est vraie alors P (n + 1) est vraie (ici il déduit P (4) de P (3)) ; enfin, il conclut que P (n) est vraie pour tout entier n ≥ 1.
Vers plus de rigueur
On trouve un autre exemple d’un raisonnement presque par récurrence, qui selon Hara Kokiti, dans Pascal et l’Induction mathématique (Revue d’histoire des sciences et de leurs applications, 1962), serait antérieur au Traité du triangle arithmétique. Pascal veut formuler un critère de divisibilité d’un nombre donné par un autre nombre en considérant les chiffres du premier nombre (voir article « Un cadeau bien enrubanné »). Il établit, en utilisant le calcul littéral, un critère valable pour un dividende à un chiffre, puis à deux chiffres et ensuite à trois chiffres et il conclut par : « La démonstration serait la même si le nombre donné se composait de plus de trois chiffres. » Ainsi, une nouvelle fois, le raisonnement par récurrence est démarré mais pas achevé ; ici la difficulté porterait sur les symboles à utiliser : comment noter un dividende à n chiffres ? Seule l’utilisation des indices permettrait une démonstration totalement rigoureuse.
L’article de Bussey de 1917 commence par : « Une critique souvent formulée des mathématiques comme sujet d’étude dans nos écoles supérieures et collèges est qu’elles n’introduisent aucune observation, expérience ou induction à la manière des sciences de la nature. » Cette critique n’est pas tout à fait justifiée : la « preuve » par l’exemple, bien qu’insuffisante, semble permettre de découvrir de nouveaux résultats, mais c’est souvent avec un raisonnement par récurrence que l’on obtiendra un résultat absolument général. Cela suppose l’utilisation du calcul littéral et, souvent, l’introduction des indices, des étapes franchies plus tard, difficilement, par les mathématiciens.
références
Œuvres complètes. Blaise Pascal, Le Seuil, 1963. Itération et récurrence. Bibliothèque Tangente 76, 2021.