
Il est souvent d’usage de dater la naissance des probabilités en 1654. Cette année-là, Blaise Pascal et Pierre de Fermat échangent de nombreux courriers relatifs à des questions liées aux jeux de hasard. Bien qu’il soit publié plus tard, c’est aussi à ce moment-là que Blaise Pascal écrit son Traité du triangle arithmétique avec quelques autres petits traitez sur la mesme matière (voir article « Les propriétés du triangle arithmétique »), dans lequel il expose les mêmes solutions. Le plus fameux de ces problèmes, dit « des partis », n’est en fait pas totalement nouveau. Plusieurs savants italiens, dont Luca Bartolomes Pacioli (vers 1447‒1517), Jérôme Cardan (1501‒1576) ou Niccolo Fontana, dit Tartaglia (1499‒1557), s’y sont déjà intéressés. Pierre de Fermat (vers 1601 ‒ 1665) en a proposé une solution assez calculatoire. Mais Blaise Pascal apporte une nouvelle vision, une « géométrie du hasard » dont la clarté frappe ses contemporains.
Une question à mille pistoles
Quel est donc ce problème des partis, proposé par Antoine Gombaud, chevalier de Méré, au déjà célèbre Blaise Pascal, alors âgé de 31 ans ? La situation met en prise deux joueurs, A et B, dans un jeu de pur hasard. Pensez par exemple à pile ou face, à la bataille, au jeu de l’oie, voire à pierre-feuille-ciseau. Chacun met en jeu la même somme d’argent. Le vainqueur sera celui qui remportera le premier un certain nombre de parties, disons trois. Mais comment répartir les gains si les deux protagonistes doivent quitter le jeu avant que l’un ou l’autre des joueurs n’ait atteint la victoire ? Par exemple, si A mène de deux parties à une ? Dans ce cas, on est enclin à donner plus à A qu’à B, mais combien exactement ?
Dans la partie de son traité consacrée à l’ « usage du triangle arithmétique pour déterminer les partys qu’on doit faire entre deux joueurs qui jouent en plusieurs parties », Blaise Pascal fixe clairement le contexte. « La première chose qu’il faut considérer est que l’argent que les joueurs ont mis au jeu ne leur appartient plus, […] ils ont reçu en revanche le droit d’attendre ce que le hasard leur en peut donner, suivant les conditions dont ils sont convenus d’abord. Mais comme c’est une loi volontaire, ils la peuvent rompre de gré à gré, et ainsi en quelque terme que le jeu se trouve, ils peuvent le quitter, et, au contraire de ce qu’ils ont fait en y rentrant, renoncer à l’attente du hasard, et rentrer chacun en la propriété de quelque chose. Et en ce cas, le règlement de ce qui doit leur appartenir doit être tellement proportionné à ce qu’ils avaient droit d’espérer de la fortune, que chacun d’eux trouve entièrement égal de prendre ce qu’on lui assigne ou de continuer l’aventure du jeu, et cette juste distribution s’appelle le parti. »
Pourquoi des « partis » pour des « parties » ?
Même si le jeu de hasard considéré ici se joue en plusieurs parties, on parle bien de problème des « partis » et Pascal écrivait même « partys ». Pourquoi pas de « e » dans cette locution ? Eh bien parce que le mot « parti » fait en fait référence à la répartition des sommes misées. Le mot « partir » vient du latin partire, qui signifie « partage ». Ce sens semble avoir disparu aujourd’hui mais on le trouve encore dans les mots « départir », « répartir » ou dans l’expression « avoir maille à partir avec quelqu’un ». Partir d’un lieu consiste cependant à s’en séparer, et on retrouve bien l’idée première du mot. Et après tout, les jeux de hasard étaient très appréciés lors des… surprises-parties !
Avant de résoudre le problème à proprement parler, Pascal énonce deux principes liés à ce qu’on appelle aujourd’hui l’espérance. Ces deux principes sont somme toute assez naturels. Tout d’abord, « si un des deux joueurs se trouve en telle condition, que quoi qu’il arrive, une certaine somme lui doit appartenir en cas de perte et de gain, sans que le hasard la lui puisse ôter », alors il ne doit pas la partager. Le deuxième principe affirme que, dans un jeu de pur hasard, si « les deux joueurs se trouvent en telle condition, que si l’un gagne il lui appartiendra une certaine somme, et s’il perd elle appartiendra à l’autre » et s’il y a « autant de hasards pour l’un que pour l’autre », alors le partage juste consiste à « [séparer] la somme qui est au hasard par la moitié, et que chacun prenne la sienne ».
Blaise Pascal précise encore les choses dans deux corollaires. Dans le premier, il déduit de ses principes que si une somme S revient à un joueur en cas de perte et que la somme S + T lui revient en cas de gain, alors le parti est qu’il prenne S + ½T. Le deuxième corollaire, équivalent au premier, consiste à démontrer que le partage des mises « peut se faire de cette façon […], que l’on assemble les deux sommes de gain et de perte, et que le premier prenne la moitié de cette somme ».
Une approche récursive
Armé de ces petits résultats bien identifiés et clairement énoncés, Blaise Pascal peut s’attaquer sereinement au problème initial. Toutefois, avant de décrire sa méthode, le grand penseur pointe précisément l’un des obstacles à la résolution du problème. Contrairement à ce que dicte souvent l’intuition aux personnes se frottant à l’épineuse question pour la première fois, il ne faut pas avoir égard au nombre des parties que les joueurs ont déjà gagnées, mais plutôt à celles qui restent à gagner à l’un et à l’autre. En effet, « deux joueurs se trouvent en même état, quand jouant en deux parties, l’un en a une à point, que deux qui jouent en douze parties, l’un en a onze à dix ». Et Pascal de proposer une reformulation plus explicite de la fameuse devinette : « Étant proposés deux joueurs, à chacun desquels il manque un certain nombre de parties pour achever, faire le parti. »
Dans les premières pages de son traité consacré au triangle arithmétique, le mathématicien a déjà formulé les premiers raisonnements par récurrence (voir article « Un orfèvre du raisonnement par récurrence »). Il poursuit ici en décrivant un parfait exemple d’algorithme récursif !
Pour bien commencer, il faut définir des cas de base. Pascal s’y emploie et signale la trivialité de ces situations : « Pour faire la chose générale sans rien omettre, je la prendrai par le premier exemple, qu’il est peut-être mal à propos de toucher, parce qu’il est trop clair, je le fais pourtant pour commencer par le commencement. » Ce cas consiste simplement à affirmer que si un joueur a déjà remporté le nombre de parties voulu et qu’il en manque à l’autre, alors le premier remporte l’intégralité des mises. Le deuxième cas de base concerne les situations où les deux joueurs sont à égalité : il suffit alors de séparer les mises en deux parts égales.
Pour la suite, Pascal explique sa méthode sur des cas particuliers, qui se généralisent facilement. Prenons le cas où il manque une partie au joueur A et deux au joueur B. Deux situations se présentent pour la prochaine partie :
• soit A emporte cette manche, et la victoire avec, et il empoche donc la totalité des mises ;
• soit B emporte cette manche et les deux joueurs se retrouvent à égalité, et se partagent donc équitablement les mises.
Si la totalité de la somme mise en jeu est de huit pistoles, comme le suggère Pascal, le joueur A va donc remporter soit huit pistoles, soit quatre, soit, d’après le deuxième corollaire, (8 + 4) / 2 = 6 pistoles.
Restons avec une somme de huit pistoles à partager et considérons maintenant qu’il manque une partie à A et trois à B. Si A gagne la prochaine manche, il remporte la victoire, soit huit pistoles. Si c’est B qui gagne la prochaine manche, il manquera une partie à A et deux à B ; on se retrouve dans le cas précédent où A remportait alors six pistoles. En appliquant le deuxième corollaire, on établit que A doit se voir attribuer (8 + 6) / 2 = 7 pistoles.
Si jamais il avait manqué une partie à A et quatre à B, le même raisonnement donne sept pistoles et demie à A et une demie pistole à B. Et l’on continue « ainsi s’il manque une partie à l’un, et cinq à l’autre, et à l’infini ».
Que faire s’il manque deux parties à A et trois à B ? Si A emporte la prochaine manche, il ne lui manquera plus qu’une partie et trois pour B ; ce cas a déjà été traité et il attribue sept pistoles à A. Si c’est B qui remporte la prochaine manche, les deux joueurs seront à égalité et A gagnera donc quatre pistoles. Finalement, on doit attribuer (7 + 4) / 2 = 5,5 pistoles à A.
Dans le cas général, « on fera les partis […] en prenant toujours ce qui appartient en cas de gain et ce qui appartient en cas de perte, et assignant pour le cas de parti la moitié de ces deux sommes ».
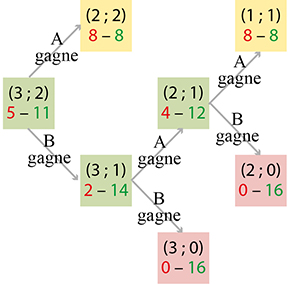
Sur ce schéma, (3 ; 2) indique qu’il reste
trois parties à gagner pour A et deux pour B.
La somme indiquée en rouge est celle qui revient à A pour une mise de départ de huit pistoles (soit seize pistoles en jeu au total), et celle en vert à B.
Avec le fameux triangle
Le recours au triangle sur un exemple
Le fameux triangle de Pascal permet de répondre rapidement au problème des partis. Prenons le cas où il manque deux parties à A et quatre à B. La base du triangle qui contient autant de cellules qu’il manque de parties aux deux joueurs ensemble (soit six) est ici la sixième ligne. En partant du début de la ligne, prenons autant de cellules qu’il manque de parties à B, c’est-à-dire 4, et additionnons-les. On trouve 1 + 5 + 10 + 10 = 26. Il reste donc deux cellules pour A, qui totalisent 5 + 1 = 6. Ces deux valeurs fournissent finalement la répartition à suivre : 26 / (26 + 6) = 13/16 des mises à A et 3/16 à B.
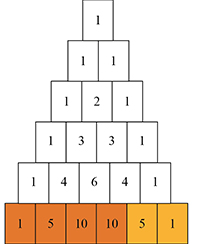
Blaise Pascal ne s’arrête pas là et propose une autre façon de procéder. Il opère ici un premier saut épistémologique. Jusqu’à présent, il a raisonné en termes d’espérance, mais là, il considère maintenant les « portions de la somme » misée gagnées, exprimées « par des fractions ». Nous y voyons aujourd’hui clairement l’expression de probabilités !
Que nous dit Pascal de ces fractions ? Si l’on note fg la fraction de la somme qui reviendrait à A en cas de gain lors de la prochaine manche et fp celle qui lui reviendrait en cas de perte, il faut lui attribuer la fraction ( fg + fp ) / 2. Pascal va même jusqu’à expliquer comment calculer cette nouvelle fraction : « Soient réduites les deux fractions à même dénomination si elles n’y sont pas, soit prise une fraction dont le numérateur soit la somme des deux numérateurs, et le dénominateur double des précédents. Cette fraction exprime la portion qui appartient au premier sur la somme qui est au jeu. » Cette précision n’est pas totalement gratuite ou destinée à des lecteurs peu familiers des fractions : c’est exactement le calcul qui intervient quelques lignes plus loin dans sa démonstration.
Alors, comment calculer rapidement la répartition des gains entre les deux joueurs ? Admettons qu’il manque a parties à A et b à B. La fraction qui revient à A est la somme des b premières cellules par rapport à la somme de toutes les cellules de la (a+b)ième ligne du triangle de Pascal. Le savant de Clermont écrit alors : « Quoique cette proposition ait une infinité de cas, je la démontrerais néanmoins en peu de mots par le moyen de deux lemmes », lesquels sont en fait l’initialisation et l’hérédité d’un raisonnement par récurrence sur le nombre total de parties manquant aux deux joueurs.
S’il manque une partie à chaque joueur, la propriété est évidente.
Supposons maintenant que la propriété soit vraie dans le cas où il manque en tout quatre parties aux deux joueurs. Imaginons qu’il manque deux parties à A et trois à B. Prenons les notations de Pascal lui-même, même si elles nous semblent aujourd’hui quelque peu exotiques.
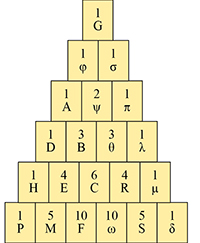
Si A gagne la prochaine manche, il ne lui en manquera plus qu’une et toujours trois à B. Par hypothèse de récurrence, on sait donc que la fraction qui revient à A est
Si A perd la prochaine manche, il lui en manquera toujours deux et il n’en manquera plus que deux à B. Par hypothèse de récurrence, on sait donc que la fraction qui revient à A est
La fraction qui revient à A est donc . En appliquant les septième et dixième conséquences du traité sur le triangle arithmétique (voir encadré), on en déduit que cette fraction est égale à :
D’où l’on conclut « que toutes les bases du triangle arithmétique ont cette propriété, car la seconde l’a par le premier lemme, donc par le second lemme, la troisième l’a aussi, et par conséquent la quatrième, et aussi à l’infini ». La clarté du discours de Pascal nous éblouit encore aujourd’hui !
Deux conséquences du traité
Deux propriétés du triangle arithmétique sont essentielles ici. La septième conséquence de la première partie du traité affirme que la somme des cellules de chaque ligne est le double de celle des cellules de la ligne précédente (voir article « Les propriétés du triangle arithmétique »).
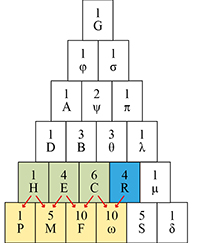
La dixième conséquence est exprimée ainsi par Pascal : « En tout triangle arithmétique, la somme de tant de cellules continues qu’on voudra de la base, à commencer par une extrémité, est égale à autant de cellules de la base précédente, plus encore à autant hormis une », à savoir la dernière. Éclairons cet énoncé sur un exemple. Dans la sixième ligne, on a :
P + M + F + ω = H + (H + E) + (E + C) + (C + R) = 2H + 2E + 2C + R.
Et avec la loi binomiale ?
Le traité de Pascal est parfois perçu comme étant une première mise en œuvre de la loi binomiale. Comme on a pu le voir ici, la formalisation n’est tout de même pas aussi nette que cela et il faudra attendre l’Ars conjectandi de Jacques Bernoulli (1654‒1705) pour y parvenir.
Comment s’écrivent les choses dans ce cas ? Notons a le nombre de parties manquantes à A, et b le nombre de celles manquant à B. Pour être certain d’avoir un gagnant, il suffit donc de jouer encore n = a + b – 1 parties, quitte à ce que l’un des deux joueurs gagne plus de parties qu’il n’en faut. Notons X la variable aléatoire égale au nombre de parties gagnées par A sur ces n prochaines parties : X suit la loi binomiale de paramètres n et 1 / 2. La probabilité P (X ≥ a) que A l’emporte est donc égale à . On retrouve bien sûr le résultat annoncé par Pascal.
références
• La saga des grands moments mathématiques : l’émergence du calcul des probabilités. Tangente 193, 2020. • Pierre de Fermat, un savant hors normes. Tangente 163, 2015. • La théorie des jeux. Bibliothèque Tangente 46, 2013. • Dossier « Les paris ». Tangente 136, 2010.


