Lorsque l’on parle de « la » moyenne de deux valeurs a et b, tout le monde comprend en général qu’il est fait référence à la moitié de la somme de a et b. Cette approche est certes la plus courante, mais pas forcément la plus appropriée. Prenons le cas d’un produit dont le prix augmente de 10 % une année et de 50 % la suivante. En allant vite en besogne, on pourrait être tenté de dire que la hausse moyenne est de 30 % par an. Cependant, enchaîner deux hausses de 30 % revient à multiplier par 1,32, soit 1,69. Autrement dit, cela correspond à une hausse de 69 %. Et pourtant, enchaîner les hausses de 10 % et 50 % revient à multiplier par 1,1 ×1,5 = 1,65, ce qui correspond à une hausse de « seulement » 65 %. La « hausse moyenne » n’est donc pas égale à 30 %. Comment la trouver alors ? Eh bien, en passant par le coefficient multiplicateur k qui doit vérifier k 2 = 1,65 et vaut donc environ 1,284, ce qui correspond finalement à une hausse de 28,4 %. Ce coefficient k est la moyenne géométrique de 1,1 et 1,5.
Des petits dessins
Dans notre exemple, la moyenne arithmétique, c’est-à-dire la moyenne usuelle, de 1,1 et 1,5 vaut (1,1 + 1,5)/2 = 1,3 et est donc supérieure à la moyenne géométrique (environ 1,284). Cela est-il toujours vrai ? Si on se donne deux nombres positifs x et y, a-t-on obligatoirement
La réponse est oui, et il suffit de mettre au carré les deux membres de cette inégalité pour s’en convaincre algébriquement. Mais quoi de mieux qu’un petit dessin pour comprendre ? Tracez un segment de longueur x + y et construisez un demi-cercle sur ce segment. Le rayon r de ce demi-cercle est la moyenne arithmétique de x et y. Où se cache la moyenne géométrique ? Il s’agit de la hauteur h du triangle rectangle ABC. En effet, l’incontournable théorème de Pythagore indique que
(x 2 + h 2 ) + (y 2 + h 2 ) = (x + y) 2.
Il ne reste plus qu’à développer et simplifier pour obtenir
Le dessin parle de lui-même : h est plus petit que r et, pour obtenir l’égalité, il faut et il suffit que x et y soient égaux.
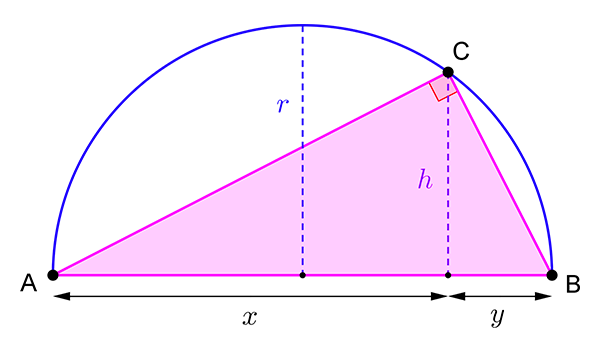
L’inégalité arithmético-géométrique devient évidente sur un dessin.
Puisque nous en sommes à jouer avec la géométrie élémentaire, que nous enseigne notre inégalité ? Si la valeur de la somme x + y est fixée, le produit xy est maximal quand x = y. Autrement dit, parmi tous les rectangles dont le périmètre est fixé, celui qui a la plus grande aire est le carré. En fixant la valeur du produit, on constate aussi que, parmi tous les rectangles d’aire donnée, celui qui a le plus petit périmètre est le carré.
Voilà un autre petit dessin pour montrer cette inégalité entre moyennes. Sur la figure suivante, la surface du grand carré est supérieure à celle des quatre rectangles :
on a (x + y)2 ≥ 4xy, ce qui donne bien
Le cas d’égalité s’obtient si le petit carré central est réduit à un point, donc si x = y.

À la Cauchy
On peut bien sûr calculer des moyennes arithmétiques et géométriques pour plus de deux valeurs positives. L’inégalité arithmético-géométrique, que l’on notera maintenant In, reste alors vraie :
Le prolifique mathématicien français Augustin Louis Cauchy (1789‒1857) en propose une jolie démonstration à la toute fin de la note II de son fameux Cours d’analyse de 1821. Marchons sur ses pas pour en comprendre le mécanisme.
L’inégalité étant établie pour deux nombres, il n’est pas difficile de l’obtenir pour quatre.
Appliquons une première fois l’inégalité I2 :
a1 a2 a3 a4 = (a1 a2 )(a3 a4 )
Appliquons encore une fois l’inégalité I2 :
Ce procédé permet de démontrer par récurrence que l’inégalité In est bien vraie pour les indices qui sont une puissance de 2 (soit n de la forme 2m).
C’est ici que Cauchy propose une méthode tout à fait étonnante, une sorte de « récurrence qui avancerait par grands bonds en avant pour reculer ensuite par petits pas afin de n’oublier aucun cas ». Prenons un entier n qui n’est pas une puissance de 2 et un entier m tel que n < 2m.
Par commodité, et comme le fait Cauchy lui-même, notons K la moyenne arithmétique des nombres a1 à an :
Complétons la liste a1, a2… an par 2m ‒ n valeurs égales à K. L’inégalité I 2m peut s’appliquer :
Or a1 + a2 +… + an = nK ; le membre de droite vaut donc . Finalement, tout se simplifie pour donner a1a2…an ≤ Kn, ce qui est bien l’inégalité In.
Les applications récréatives ne manquent pas. Un instant de réflexion vous permettra de vous convaincre que la somme d’un nombre réel positif et de son inverse est supérieure ou égale à 2 : si x > 0, alors
Sans beaucoup d’effort, l’inégalité arithmético-géométrique vous permettra d’établir que si l’on considère des nombres positifs ai, on a aussi et, plus généralement,
À la Liouville
L’approche de Cauchy est très algébrique. Quelques années plus tard, en 1839, Joseph Liouville (1809‒1882) propose dans le Journal de mathématiques pures et appliquées, qu’il a lui-même créé en 1836, une autre démonstration adoptant un point de vue plus analytique. Il s’agit cette fois-ci d’une récurrence tout à fait classique.
Regardons comment obtenir l’inégalité I3 lorsque I2 est connue.
Le but est de démontrer que, trois réels x, y et z étant donnés,
ou, dit autrement, que
Pour cela, posons
Le but est de montrer que cette fonction est positive, ce qui est une question bien classique.
Calculons la dérivée.
On a et cette dérivée est croissante sur ] 0, + ∞ [.
Elle s’annule en
La fonction f atteint donc son minimum en xm et un calcul un peu laborieux, mais sans astuce, fournit
L’inégalité I2, à savoir nous indique que ce minimum est positif ou nul. L’affaire est pliée ! Il reste le cas d’égalité à traiter. Le minimum de f vaut 0 si, et seulement si, y = z (c’est le cas d’égalité pour I2) et, dans ce cas, on a
Avec un peu plus de formalisme, mais sans autre difficulté conceptuelle, la méthode de Liouville permet de démontrer que si In est vraie pour un certain entier n, alors In+1 l’est aussi.
Des moyennes et des suites
La moyenne arithmétique est plutôt utilisée dans des domaines où l’on étudie des phénomènes qui suivent un modèle linéaire. Dans une suite arithmétique, chaque terme est la moyenne (arithmétique) de celui qui le suit et de celui qui le précède. La moyenne géométrique est quant à elle plutôt utilisée dans des domaines où l’on étudie des phénomènes qui suivent un modèle exponentiel. Si (un )n ≥ 0 est une suite géométrique, le terme un est d’ailleurs la moyenne géométrique de un‒1 et un+1. On peut calculer des moyennes pondérées pour n valeurs dans les deux situations. Pour la moyenne arithmétique, la formule est bien sûr
La version analogue pour la moyenne géométrique est
À la Jensen
Alors qu’elle semble au premier abord purement algébrique, l’inégalité arithmético-géométrique s’invite donc en analyse.
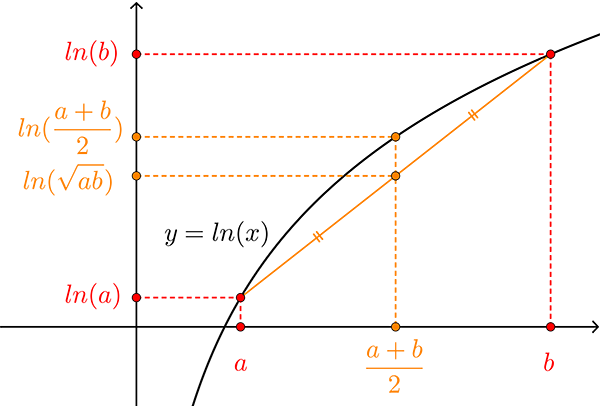
Comme elle établit un lien entre addition (pour la moyenne arithmétique) et multiplication (pour la moyenne géométrique), on est naturellement invité à y voir un lien avec le logarithme népérien, mais lequel ?
Voyons sur le cas le plus élémentaire, celui qui fait intervenir deux nombres positifs a et b.
On a ce qui revient à affirmer que
est supérieur à
qui vaut en fait
Ceci n’est que la traduction de la concavité de la fonction ln !
La fonction ln est concave.
On peut même en déduire une deuxième inégalité pour le cas des moyennes pondérées :
si a1, a2, x1 et x2 sont des réels strictement positifs,
on a :
et donc
Cette remarque se généralise-t-elle à l’inégalité In pour tout entier n supérieur ou égal à 2 ? Oui, et c’est même un résultat plus fort encore qui nous a été offert au début du XXe siècle. En 1906, la célèbre revue Acta Mathematica, fondée par le Suédois Gösta Mittag-Leffler (1846‒1927), propose un article rédigé en français et intitulé Sur les fonctions convexes et les inégalités entre les moyennes. Il est signé d’un ingénieur danois, Johan Ludwig William Valdemar Jensen (1859‒1925), qui s’intéresse de près à la théorie des fonctions et reprend ici une conférence donnée à la Société mathématique danoise le 17 janvier 1905.
Jensen établit que, si φ est une fonction convexe sur un intervalle et si x1, x2… xn sont des réels de cet intervalle, alors on a
Pour justifier ce résultat, Jensen s’inspire de Cauchy et opère par une sorte de « récurrence à rebours ». Il établit d’abord que la propriété est vraie pour tout entier n égal à une puissance de 2, par une récurrence classique, puis en déduit (par un artifice tout à fait similaire à celui de l’auteur du Cours d’analyse de 1821) que, si son inégalité est vraie pour un certain entier n, elle est vraie pour tout entier qui lui est inférieur.
Avec la formule de Héron
Les sommes et les produits de nombres peuvent rappeler des calculs de périmètres ou d’aires en géométrie, où l’inégalité arithmético-géométrique apporterait d’intéressants renseignements. Prenons le cas des triangles. La célèbre formule de Héron, du nom d’un formidable ingénieur et mathématicien du Ier siècle ayant vécu en Égypte (voir notre dossier « La formule de Héron » dans Tangente 180, 2018), nous indique que, dans un triangle de côtés a, b, c, on a la relation où S est l’aire du triangle et p son demi-périmètre.
En appliquant l’inégalité arithmético-géométrique aux nombres p ‒ a, p ‒ b et p ‒ c (dont la somme vaut tout simplement p), on constate que (p ‒ a)(p ‒ b)(p ‒ c) est inférieur à (p/3)3. Ce résultat, couplé à la formule de Héron, indique finalement que
Conformément à l’intuition que l’on peut en avoir, l’égalité a lieu pour les triangles équilatéraux, et uniquement ceux-là. Ce sont donc les triangles d’aire maximale pour un périmètre donné.
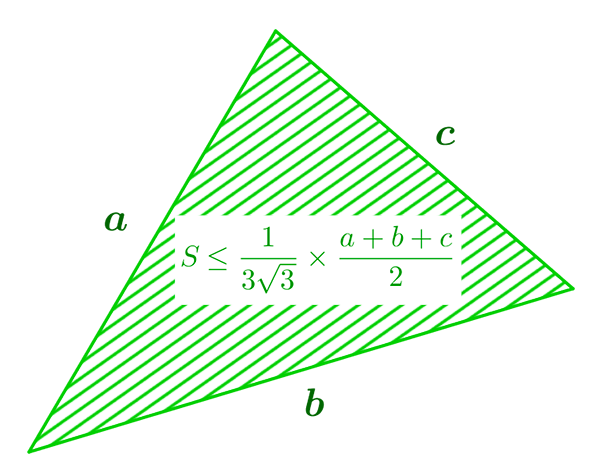
L’aire d’un triangle est toujours inférieure ou égale
au quotient du carré de son demi-périmètre par 3 √ 3 .
Cela étant établi, l’utilisation de limites astucieuses permet de généraliser encore plus l’inégalité.
En effet, on se convainc facilement que
où les coefficients mi, pour i variant de 1 à n, sont des entiers.
Cette inégalité reste encore vraie avec des pondérations non entières ! Prenons n réels positifs a1, a2… an. Si l’on suppose la fonction φ continue en plus d’être convexe, et à l’aide d’une démonstration un peu sophistiquée, on obtient l’inégalité de Jensen :
De nos jours, on dirait simplement que le résultat se généralise par densité de ℚ dans ℝ. Et si la fonction est concave, il suffit de renverser l’inégalité.
Il semblerait que tant d’abstraction nous ait éloignés de notre inégalité arithmético-géométrique… mais prenons la fonction ln, qui est concave, et posons pour i variant de 1 à n.
Dans ce cas, la somme vaut 1 et, après quelques simplifications, on obtient bien :
Finalement, derrière nos petits dessins de début d’article se cachent des généralisations bien plus spectaculaires !
Pour étudier une célèbre limite
Tout lycéen de terminale se doit d’avoir étudié la suite définie, pour tout entier naturel non nul n, par
Même le jeune Galois s’y est collé (voir Évariste Galois, Bibliothèque Tangente 82, 2023).
Montrer que cette suite est croissante n’est pas chose aisée pour les débutants. L’inégalité arithmético-géométrique permet de s’en tirer à moindres frais, il « suffit » de voir à quels nombres on doit l’appliquer. Le choix judicieux consiste à prendre le réel 1 puis le réel répété n fois. Faites le calcul pour vous en convaincre !
La concavité de la fonction ln peut s’inviter une nouvelle fois ici pour démontrer que la suite est majorée. Pour tout réel strictement positif x, on a ln(1+x) ≤ x et donc
Croissante et majorée, cette suite converge !
Quand Jensen revient à Cauchy
Dans son article de 1906, Johan Jensen évoque, dès les premières lignes, la démonstration de l’inégalité arithmético-géométrique par Cauchy et en salue le caractère élégant, qui lui a permis de traverser les âges sans modifications particulières. Cauchy est aussi connu pour une autre inégalité qui porte aujourd’hui son nom, l’inégalité de Cauchy‒Schwarz, et qui correspond elle aussi à un cas particulier de l’inégalité de Jensen. En effet, prenez la fonction carrée, qui est convexe, remplacez les réels ai par leurs carrés et les xi par (le cas où ai = 0 ne présente pas d’intérêt majeur ici).
Vous en déduirez que