
Quand on entreprend la construction des principaux ensembles de nombres, on part en général des entiers puis des rationnels, quotients d’entiers, pour ensuite remarquer qu’une expression comme ne peut pas s’écrire sous forme de fraction. Souvent, à peine cette observation faite, on s’empresse de remarquer que
et leurs petits camarades tels que
ou
sont également irrationnels. Ils peuvent donc eux aussi prétendre à une place dans le monde des nombres, élargissant considérablement les frontières de ce dernier.
Or plutôt que de se lancer d’emblée dans une exploration aussi immense, on peut s’arrêter à ce qui se passe quand une seule racine carrée est introduite. De cette manière se révèlent les corps quadratiques. Ces régions particulières disposent de leurs structures propres, qui prolongent de façon étonnamment régulière celle de l’ensemble des nombres rationnels.
Les corps quadratiques prolongent la structure de l'ensemble des rationnels
Voyons pour commencer le cas de . Nous partons de l’ensemble ℚ des nombres rationnels (ceux qui peuvent s’écrire sous la forme d’un quotient a/b avec a et b entiers), et nous lui adjoignons
ainsi que tous les nombres que
et les rationnels permettent d’engendrer à partir des quatre opérations de l’arithmétique : addition, soustraction, multiplication et division. L’ensemble des nombres ainsi obtenu se note ℚ(
). Cette façon d’étendre l’ensemble des fractions à partir d’une racine carrée constitue une extension quadratique. Par construction, l’ensemble ainsi défini dispose d’une structure de corps (voir encadré).
La notion de corps
Considérons une partie E de l’ensemble des nombres réels. Cette partie E est un corps dès lors qu’elle contient 0 et 1 et qu’elle est stable par les quatre opérations. Autrement dit, E est un corps lorsque, quels que soient deux de ses éléments e et e’, les valeurs e + e', e – e', e × e' et e/e' sont aussi des éléments de E (on interdit tout de même la division par 0). Comme nous sommes dans l’ensemble des nombres réels, les propriétés usuelles (commutativité et associativité) de l’addition et de la multiplication sont vérifiées.
Puisque E doit contenir 1, il doit aussi contenir 1 + 1 = 2, et donc aussi 1 + 2 = 3, et donc tous les entiers naturels. Ensuite, par soustraction il doit aussi contenir 0 – 1, 0 – 2, etc., c’est-à-dire tous les entiers négatifs. Enfin, par division, il doit aussi contenir tous les nombres rationnels. Ainsi donc, quel que soit le corps E constitué de nombres réels, on a l’inclusion : ℚ ⊂ E.

Parmi les nombres réels, l’ensemble ℚ est le plus petit corps. Il est inclus dans le corps ℚ ( 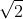 ), qui est lui-même le plus petit corps contenant
), qui est lui-même le plus petit corps contenant 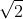 . Un corps plus gros, qui contient tous les ℚ (
. Un corps plus gros, qui contient tous les ℚ (  ), est le corps
), est le corps  ℝ des nombres algébriques réels. Lui-même est inclus dans le corps ℝ des nombres réels.
ℝ des nombres algébriques réels. Lui-même est inclus dans le corps ℝ des nombres réels.
L’allure d’un corps
En plus de contenir les nombres rationnels eux-mêmes, ℚ( ) contient aussi l’ensemble des nombres de la forme
, où r est un rationnel. En combinant par addition ces deux types de nombres, on obtient les nombres de la forme q + r
(avec q et r rationnels).
Les choses ont donc tendance à se compliquer à mesure que nous faisons des opérations nouvelles, ce qui n’est pas une surprise a priori. Pourtant, une surprise nous attend bel et bien : il se trouve que les opérations ultérieures, elles, ne compliqueront plus les choses.
Tout d’abord, lorsqu’on additionne deux nombres comme et
le résultat s’écrit
et donc il a la même forme que celle de nos deux nombres initiaux. Faute de désignation consacrée, nous parlerons ici de forme simple.
Nous venons de voir que les formes simples restent simples quand on les ajoute. Que se passe-t-il alors quand on les multiplie ?
Le résultat tient en un calcul immédiat :
Grâce au fait que le produit de par elle-même donne un entier, le produit de deux formes simples est donc lui aussi une forme simple.
Enfin, reste une dernière opération, la division. Avec une expression comme il semble bien qu’il faille aller au-delà des formes simples. Pourtant, tel n’est pas le cas.
Pour le voir, appelons conjugué de le nombre
La propriété fondamentale expliquant l’introduction de cette notion est que le produit d’un nombre par son conjugué est un nombre rationnel, en vertu de l’identité remarquable (a+b)(a–b) = a2–b2 :
Le recours au conjugué permet alors de se débarrasser d’un dénominateur encombrant, de la manière suivante :
L’expression un peu grosse finalement obtenue ne doit pas tromper : il s’agit bien, une fois encore, d’une forme simple. En effet, les deux fractions impliquées sont des sommes, différences, produits et quotients de nombres rationnels, donc encore et toujours des nombres rationnels.
Permanence d’une forme
En divisant deux formes simples, on obtient donc un nombre qui, lui-aussi, peut s’écrire sous forme simple. Cette permanence au travers des quatre opérations nous dit que tous les éléments de ℚ( )peuvent donc s’écrire sous la forme q + r
avec q et r rationnels. On peut par ailleurs démontrer que l’écriture sous forme simple est nécessairement unique (voir encadré).

Une écriture unique
Supposons qu’un même élément de ℚ( ) puisse s’écrire de deux façons sous une forme simple, et donc qu’on trouve des rationnels q, q', r et r' tels que
Bien sûr, si r = r’ alors q = q’ et les deux formes n’en font en réalité qu’une. En revanche, si r ≠ r’ alors on peut réordonner les termes de l’égalité précédente pour écrire
Puisque q, q', r et r' sont des rationnels, le membre de droite est lui aussi un nombre rationnel, ce qui n’est pas possible puisque ne l’est pas. L’hypothèse r ≠ r' n’est donc pas tenable, donc r = r' et donc, comme déjà indiqué, q = q'. Il ne peut donc pas exister deux formes simples distinctes pour un même élément de ℚ(
).
Sans grande surprise, ce qui fonctionne si bien avec fonctionne aussi avec
, et plus généralement avec
où k est n’importe quel entier sur lequel ne pèsent que des restrictions naturelles, comme, par exemple, le fait qu’il ne doit pas être un carré parfait (voir encadré).
Les bonnes racines
Le cas de ℚ( ) fonctionne comme celui de ℚ(
) , les seules nuances étant que les éléments de ℚ(
) s’écrivent tous sous la forme
et que le conjugué de
est
En revanche, il n’y a pas d’intérêt à considérer ℚ( ). En effet, puisque
est un élément de ℚ, on a tout simplement l’égalité ℚ(
) = ℚ. La même remarque vaut pour les racines carrées d’entiers qui sont des carrés parfaits :
etc.
D’autre part, bien que 18 ne soit pas un carré parfait, on évite de considérer ℚ( ), parce que
on a donc en fait ℚ(
) = ℚ(
). Plus généralement, on n’écrit ℚ(
) que lorsque k est quadratfrei, c’est-à-dire sans facteur carré.
Une fois ces nettoyages faits, on peut considérer les ℚ( ) restants, qui constituent toutes les extensions quadratiques distinctes possibles.
Les premières sont
ℚ( ), ℚ(
), ℚ(
), ℚ(
), ℚ(
), ℚ(
), ℚ(
), ℚ(
), ℚ(
), etc.
Pour vous exercer : à laquelle des extensions quadratiques précédentes
est égale ℚ
Non seulement ces ensembles n’ont pas les mêmes éléments (en-dehors des rationnels), mais ils ne se ramènent pas non plus les uns aux autres, au sens où il n’est pas possible, par exemple, d’envoyer les éléments de ℚ( ) sur ceux de ℚ(
) de sorte que les opérations sur les éléments du premier correspondraient exactement à celles sur leurs images dans le second.
Chacun des corps ℚ( ) ainsi obtenu est comme un monde en soi à explorer. On peut notamment s’intéresser à y redéfinir la notion d’entier. Dans ℚ(
), par exemple, les éléments qui jouent le rôle des entiers sont les nombres de la forme m + n
où m et n sont des entiers (des vrais, ceux-là !). Ils constituent l’ensemble noté
, qui dispose de propriétés extrêmement voisines de celles de ℤ. En particulier, un élément de ℤ(
) est dit premier lorsqu’il ne peut pas s’écrire comme produit de deux autres éléments de ℤ(
) (sauf si l’un des deux est une unité, c’est-à-dire l’équivalent de ce que sont 1 et ‒1 dans ℤ). On peut alors énoncer un théorème de décomposition analogue à celui qui a cours dans ℤ : tout élément de ℤ(
) s’écrit de façon unique comme produit d’éléments premiers de ℤ(
).
Les possibilités offertes par cette arithmétique d’un nouveau genre dépendent toutefois de façon décisive de la racine carrée choisie pour l’extension quadratique. En effet, on peut par exemple démontrer que l’énoncé précédent de décomposition en produit d’éléments premiers ne fonctionne pas dans ℤ( ). Dans cet ensemble, on a ainsi deux décompositions pour le nombre 6, alors que l’on peut démontrer que les quatre facteurs qui interviennent sont bien premiers (dans ℤ(
) bien sûr !) :
Ainsi, les généralisations des théorèmes classiques de l’arithmétique ordinaire ne vont pas toujours d’elles-mêmes dans ces nouveaux mondes. La richesse des corps quadratiques réside aussi dans leur diversité.
références
• Introduction à la théorie des nombres. Godfrey Harold Hardy et Edward Maitland Wright (traduction de François Sauvageot), Vuibert‒Springer, 2007.


