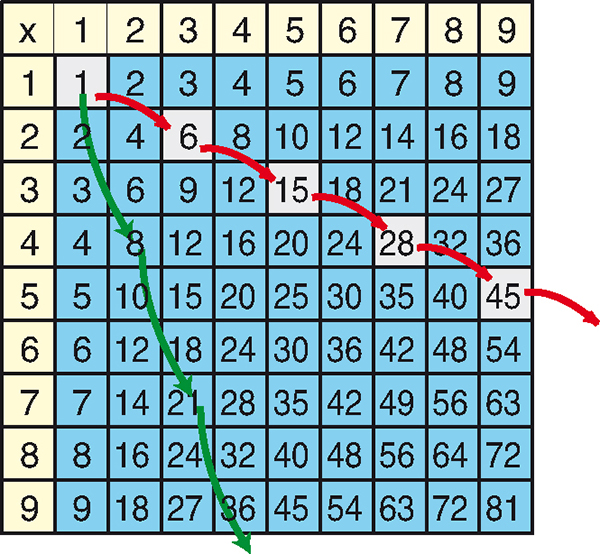
Imaginez une table de Pythagore (table de multiplication usuelle), mais infinie, permettant de multiplier n’importe quel entier par n’importe quel autre. On se déplace sur cette table à partir de la case contenant 1 (correspondant au produit 1 × 1) et on saute de case en case selon le mouvement d’un cavalier aux échecs (voir les flèches rouges de la figure). La suite commence par 1, 6, 15, 28, 45. Quel sera le vingt-et-unième terme de cette suite ?
Si l’on sait que la fonction associant à la énième case la valeur qu’elle contient est une fonction polynôme, on procède comme suit. Sur une première ligne, on écrit les nombres de la suite. Sur une deuxième, on reporte dans l’ordre les différences entre les valeurs successives des nombres de la suite. Sur une troisième ligne, on renseigne les différences successives entre ces premières différences. On continue ainsi jusqu’à l’obtention d’une suite constante, la ligne suivante n’étant constituée que de 0.

Si la énième ligne n’est constituée que de 0, alors le polynôme de plus petit degré prenant les valeurs de la première ligne est de degré n – 2. Ici, on a donc affaire à un polynôme P de degré 2, de la forme ax2 + bx + c.
On pose alors P (0) = 1, P (1) = 6, P (2) = 15, P (3) = 28, P (4) = 45. L’égalité P (0) = 1 donne c = 1. De P (1) = 6, on déduit a + b + c = 6 et a + b = 5. De P (2) = 15, on tire 4a + 2b = 14. On obtient finalement a = 2 et b = 3. Le polynôme cherché est donc P (x) = 2x2 + 3x + 1 et la vingt-et-unième case visitée (correspondant à x = 20) contiendra le nombre 861. Cet entier correspond bien au produit de 21 par 41, la case correspondante se trouvant sur la ligne 21 du tableau et dans la colonne 41.
1. Si l’on se déplace comme un chameau (pièce d’échecs féériques) qui saute selon la diagonale d’un rectangle de deux cases sur quatre (voir les flèches vertes), quel sera le nombre contenu dans la vingt-et-unième case visitée ?
Il n’y a pas que les polynômes…
Cette méthode ne donne que le polynôme de plus petit degré admettant les valeurs données, mais il existe une infinité d’autres fonctions (polynomiales ou non) admettant ces mêmes valeurs. Cette méthode correspond à des « dérivations successives dans l’ensemble des entiers ». En écrivant les dérivées successives de la fonction P(x) = 2x2 + 3x + 1, on obtient P’(x) = 4x + 3 et P’’(x) = 4. Lorsque l’on a affaire à une fonction non polynomiale, on ne parvient pas à une constante. La fonction qui à x associe 2x, par exemple, donne successivement les différences 1, 2, 4, 8, 16, 32…, qui se répètent indéfiniment.
.jpg)
Si l’on trace une droite dans le plan, celui-ci est partagé en deux régions. Avec deux droites non parallèles, le plan est partagé en quatre régions ; avec trois droites, il est partagé au maximum en sept régions ; avec quatre droites, en onze régions. Le nombre maximal de régions déterminées par n droites est une fonction polynômiale de n.
2. Quel est le nombre maximal de régions déterminées par dix droites dans le plan ?

