Certaines expressions donnent un résultat numérique « quasiment entier », comme la fameuse constante de Ramanujan, (voir Tangente 166, 2015). Mais il existe de nombreux autres exemples, tant numériques que géométriques.
Racine entière ou décimale ?
La racine carrée du nombre 111 111 111 555 555 555 n’est pas égale à un nombre entier. En effet, seuls les entiers multiples de 5 ont un carré se terminant par 5, mais tous les carrés d’entiers multiples de 5 se terminent par 25, donc aucun carré d’entier ne peut se terminer par 55. Pourtant, la calculatrice de notre navigateur Internet nous indique que est égal à 333 333 334. Or, le carré de 333 333 334 est égal à
111 111 111 555 555 556 (voir Tangente 184, 2018).
Considérons maintenant le nombre :
N = 444 444 444 222 222 2222. Aucun carré d’entier ne se termine par un 2, donc la racine carrée de N n’est pas entière. Est-elle décimale ? Changeons d’outil de calcul. Un tableur nous donne une racine carrée égale à 666 666 666,5 mais le carré d’un tel nombre devrait avoir une partie décimale égale à 0,25. Alors, que croire ?
Un calculateur de précision nous donnera « proche » de
666 666 666,499 9999 998 125, qui est effectivement « très proche » de 666 666 666,5.
Tous les nombres de la forme 444…44222…22,25 (n chiffres 4 suivis de n chiffres 2 et d’une partie décimale égale à 0,25, n étant strictement positif) sont les carrés de nombres de la forme 666…66,5 (n chiffres 6 suivis d’une partie décimale égale à 0,5). Ceci découle de l’identité suivante :
La géométrie n’est pas épargnée ! La figure suivante est due au mathématicien américain Edward Taylor Pegg Jr (né en 1963). Il s’agit ici de calculer la distance d = AD. Est-elle entière ?
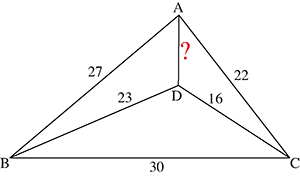
Une méthode possible est de se placer dans un repère orthonormé de sommet B et d’axe des abscisses (BC), puis de calculer les coordonnées des points A et D dans ce repère. On obtient alors soit environ 7,000 000 086. La différence avec un nombre entier est inférieure à neuf cent-millionièmes !
Le fidèle carré n’est lui-même pas à l’abri. ABCD est le carré suivant. Son côté est-il entier ?
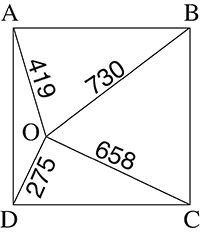
Posons OA = a, OB = b, OC = c et OD = d. En utilisant a2 + c2 = b2 + d2, on trouve que le côté l du carré est solution de l’équation suivante :
2l4 – 2(a2 + c2)l2 + (b2 – c2)2 + (b2 – a2)2 = 0, qui devient, avec les données de la figure, l4 – 608 525l2 + 68 839 182 508,5. Cette équation a pour solutions
et seule la plus grande des deux solutions correspond au cas où Pierre est à l’intérieur du carré. On trouve alors une valeur de l proche de 676,999 999 94, valeur qui diffère d’un entier de moins d’un dix-millionième.
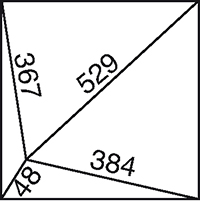
Voici un autre carré. À vous de calculer la longueur de son côté !
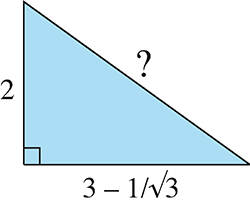
Enfin, voici un triangle rectangle tout simple. Calculez la longueur de son hypoténuse.