
Au XVIIe siècle, suite à « son » invention de la géométrie analytique (voir article "Une notion géométrique insaisissable", § Vers l'époque moderne), René Descartes sait déterminer les tangentes à une courbe géométrique donnée. Son contemporain et correspondant Pierre de Fermat (vers 1601 ; 1665), en utilisant une notion de « nombres infiniment petits », le fait pour une multitude de courbes, géométriques comme mécaniques. Prenons le folium de Descartes, une courbe qui a pour équation x3 + y3 – 3xy = 0. Il s’agit d’un exemple de courbe géométrique, dans la terminologie de Descartes, qui ne provient pas d’une construction mécanique. Avec la terminologie moderne, c’est une cubique, c’est-à-dire une courbe algébrique de degré 3. Bien que jugé difficile par Descartes, le calcul des tangentes à cette courbe fut réalisé par Fermat de manière élégante.
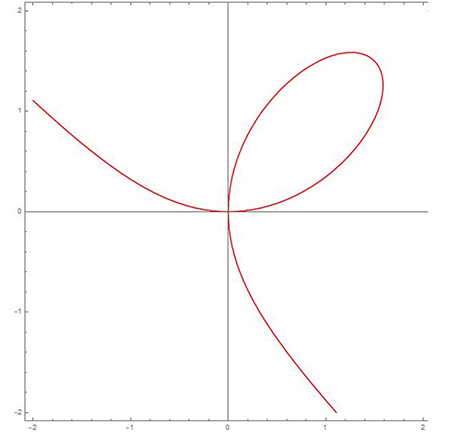
Le folium de Descartes.
C’est alors le début du calcul infinitésimal, qui va se développer avec Isaac Newton (1642–1727) et Gottfried Wilhelm Leibniz (1646–1716). Pierre-Simon Laplace (1749–1827) affirmera d’ailleurs dans son Programme : « L’un des plus féconds rapprochements que l’on ait faits dans les sciences est l’application de l’algèbre à la théorie des courbes. La recherche de ces propriétés a conduit à l’analyse infinitésimale, dont la découverte a changé la face des ... Lire la suite
