Nous commençons notre voyage par les nombres triangulaires qui constituent la base des nombres figurés.
À l’étape n, des points sont rangés sur n segments de droites parallèles aux côtés du triangle (qui peut être quelconque), ce qui fait 3n segments. Le calcul du nombre de points Tn = 1 + 2 +…+ n peut se faire par diverses méthodes, mais l’une des plus belles est certainement celle donnée par la preuve sans mots, tirée du livre Nombres et figures d’Irving Adler, et reproduite ci-dessous.
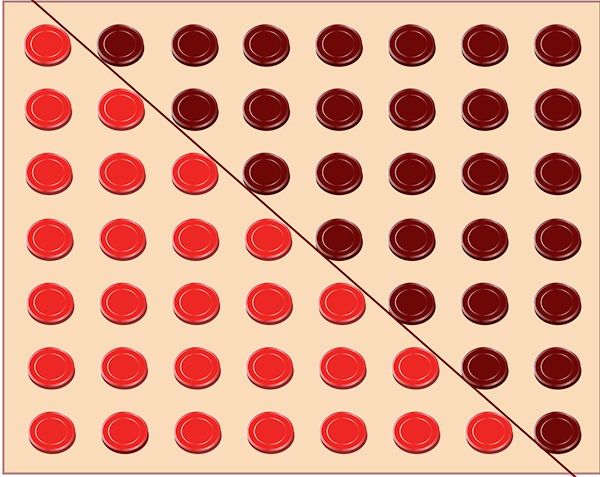
Ce rectangle de côtés n et n + 1 est partagé en deux nombres triangulaires égaux d’ordre n ce qui donne
Trois voies de construction
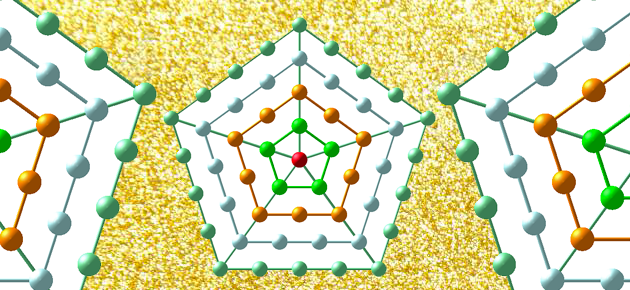
La figure suivante illustre, en prenant l’exemple de l’hexagone, comment les mathématiciens grecs ont généralisé les nombres figurés aux polygones réguliers à k côtés.
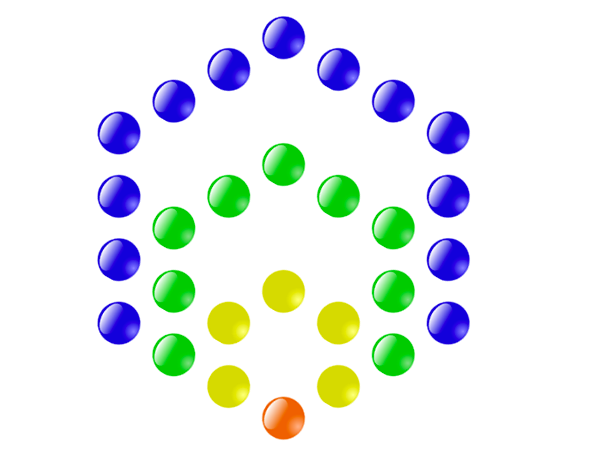
Construction des nombres hexagonaux.
Il n’y a qu’un point (rouge) à l’étape 1, et k points aux sommets d’un polygone à k côtés à l’étape 2 (points jaunes).
On choisit alors un sommet, le rouge, et on effectue une homothétie de rapport 2 centrée sur ce sommet qui permet de rajouter un point sur ... Lire la suite
