
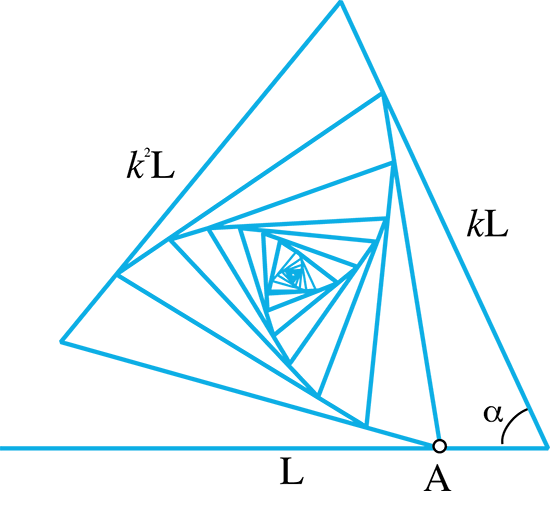
La figure suivante n’est pas un polygone. Elle a été construite à partir d’un segment de droite et d’un algorithme bien précis : dupliquer ce segment en tournant d’un angle α et en appliquant un coefficient de réduction k (ici strictement inférieur à 1) à sa longueur.
En itérant ce procédé, on obtient cette jolie structure qui converge vers un certain point du plan.
Remarquons que pour les valeurs k = 1 et α = π – 2π/n, la construction permettrait d’obtenir un polygone régulier convexe à n côtés. Certaines valeurs d’angles permettent également d’obtenir des polygones étoilés.
En dehors de ces cas particuliers, on réalise un jolygone, néologisme qui apparaît dans la revue Le petit Archimède en 1975.
Le jolygone représenté ci-dessus présente une particularité : à la troisième itération, on revient en A sur le segment de départ. On dit que ce jolygone est auto-tangent. Il a été construit avec les valeurs α = 65° et k = 0,9. Il est possible d’utiliser les nombres complexes pour étudier les jolygones. Lorsqu’un segment est représentable par un nombre complexe z, le suivant correspond au nombre zkeiα.
Référence : Le petit Archimède n°14, 1975. Disponible en ligne.

.png)