Les histonombres
Les nombres triangulaires, carrés, pentagonaux et autres sont bien connus et traités dans ce dossier. Mais quid de l’opération inverse, qui partirait d’un nombre quelconque pour le transformer en polygone ? Voyons quelques manières de fabriquer (de façon un rien artificielle, certes) de tels polygones, aux formes parfois étranges.
Une idée très naturelle consiste à représenter chaque chiffre c d’un nombre entier, en système décimal, par une colonne où l’on empile c carrés de côté unité. Polygonons ainsi 143 :
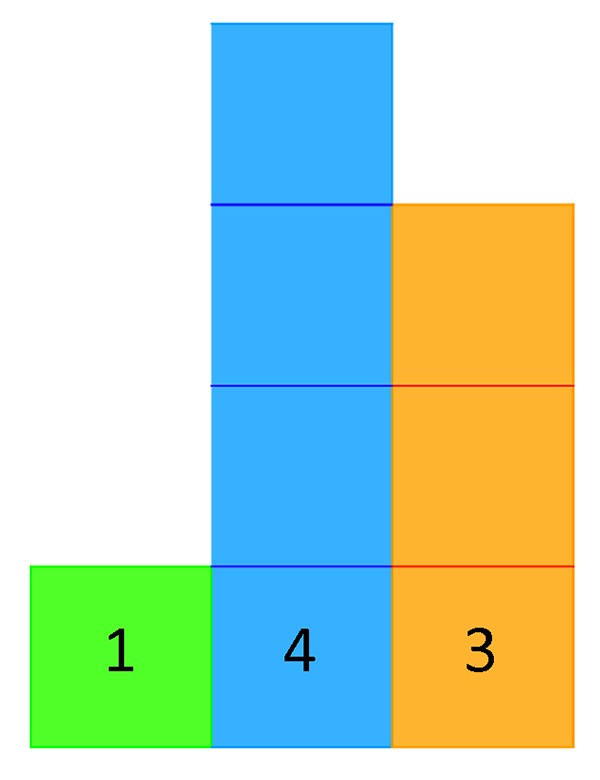
Sa surface est égale au nombre de carrés le constituant, c’est-à-dire à la somme de ses chiffres, ici 8. Pour un nombre N de n chiffres, on peut facilement vérifier que, si chacun de ses chiffres « côtoie » un chiffre plus grand, excepté bien sûr pour le plus grand Mn, son périmètre est P(N) = 2(Mn + n). Les nombres 143, 134 et leur « miroir » 341 et 431 créent donc des polygones de même surface, S = 8 (= 1 + 3 + 4), et de même périmètre, P = 14 (Mn = 4 et n = 3).
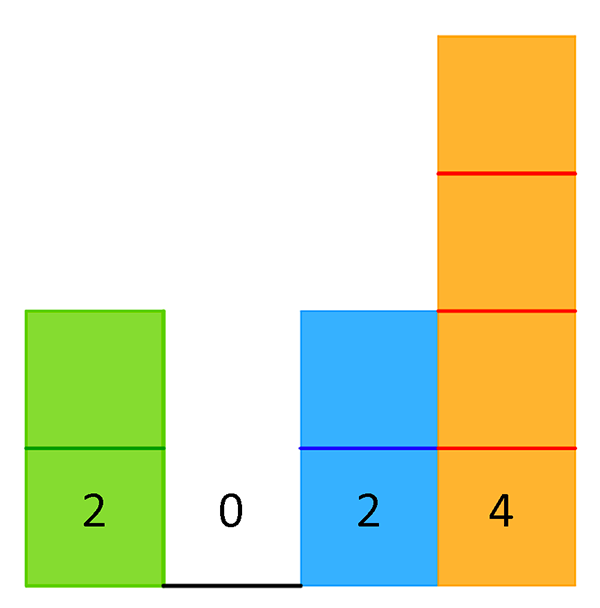
Mais que faire des nombres qui comportent un zéro ? 2024 par exemple, ou 1000 ? Polygonons-les de même :