Prenez un treillis à mailles carrées ou rectangulaires constitué de barres articulées entre elles en chaque sommet du réseau.

Ce treillis T est posé sur un plan P et la gravité lui impose un contact constant avec P. Les articulations permettent à T d'être déformable, tous en restant en contact avec P.
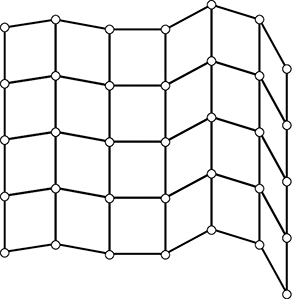
Pour rigidifier ce treillis, il est possible de lui ajouter des barres diagonales Ci-dessous, on a ajouté neuf barres diagonales.
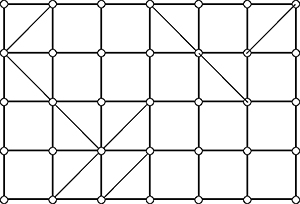
1. L'ensemble du treillis ainsi constitué est-il indéformable (dans le plan) ?
Plusieurs questions viennent à l'esprit. Déjà, quel est le nombre minimal de barres diagonales à ajouter pour rigidifier le treillis T ? Ensuite, comment vérifier si un treillis auquel on a ajouté ce nombre minimal de barres diagonales est effectivement rigide ?
Il a été démontré que le nombre minimal de barres diagonales nécessaires pour rigidifier un treillis rectangulaire de n mailles sur p mailles est égal à n + p – 1. Pour vérifier si un treillis auquel on ajouté n + p – 1 barres diagonales est bien rigidifié, on peut utiliser un algorithme réduisant, de proche en proche, le treillis à un treillis de plus en plus simple jusqu'à aboutir à un seul carré (ou rectangle) rigidifié ou non, selon le cas.
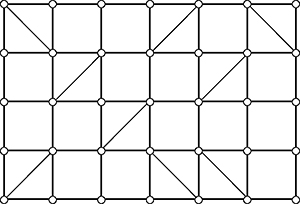
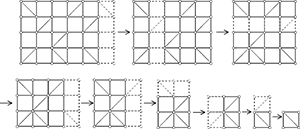
Réduction d'un treillis donné à un treillis plus simple : on élimine une à une des rangées horizontales ou des colonnes dont on sait qu'elles sont entièrement rigidifiées, jusqu'à aboutir ici à un seul carré. Ce carré étant rigidifié, l'ensemble du treillis est bien rigide.
Des généralisations sont possibles. Par exemple, comment rigidifier un treillis plan à mailles hexagonales ? On sait que pour rigidifier un polygone à n côtés, il faut le trianguler, c'est-à-dire qu'il faut lui ajouter n – 3 barres diagonales.
On peut également passer à la dimension 3, sachant que le seul solide indéformable est le tétraèdre (qui, en dimension 3, joue le même rôle que le triangle en dimension 2).
2. Combien de barres diagonales faut-il ajouter pour rigidifier un cube ?

