Le premier à avoir théorisé les relations entre mathématiques et musique semble avoir été Pythagore, pour qui la musique faisait partie intégrante des mathématiques, au même titre que l’arithmétique ou la géométrie. D’après la légende, passant près d’une forge, il entendit différents marteaux émettre des sons différents en frappant la même enclume. Intrigué, le mathématicien grec examina les marteaux et comprit que le son émis par l’enclume dépendait uniquement du poids du marteau qui la frappait. Il était possible de relier mathématiquement les valeurs des poids de deux marteaux permettant d’émettre des sons espacés d’une octave (ou de tout autre intervalle donné).
Pythagore étudia ensuite le son émis par la vibration d’une corde, qui dépend uniquement de la longueur de la corde. La fréquence d’un son est le nombre de vibrations par seconde. Ainsi, le la du diapason correspond à 440 hertz, ou 440 vibrations par seconde. Si l’on divise par deux la longueur d’une corde qui donnait un la, on obtient à nouveau un la, mais plus aigu et dont la fréquence est de 880 hertz. Les deux notes sont dites à l’unisson. Elles sont espacées d’une octave (huit degrés dans l’échelle de notes utilisée en Occident). Pythagore remarqua que les accords « les plus harmonieux » correspondaient aux rapports de longueurs les plus « simples », comme 1/2, 2/3 et 3/4.
On a ici .Les points A, B, E, D forment donc une division harmonique de l’intervalle [AD].
En combinant ces rapports et en prenant pour unité la fréquence d’une corde de longueur 1 émettant un do, on obtient le tableau suivant.
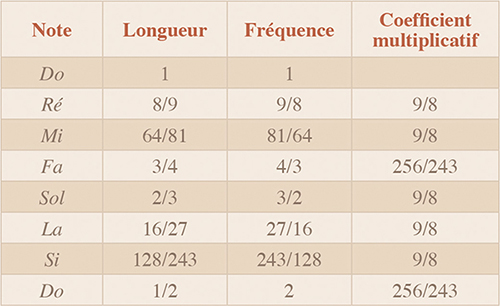
Lorsque l’on multiplie une fréquence par 9/8, on monte d’un ton. Lorsque l’on multiplie une fréquence par 256/243, on monte d’un demi-ton.
Un comma dans l’intervalle
En partant du do de fréquence 1, et en multipliant successivement par 3/2, on obtient le « cycle » suivant.
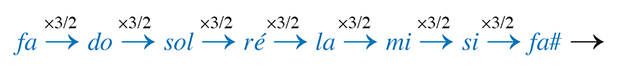
Ce pseudo-cycle se poursuivrait par do#, sol#, ré#, la#, mi#. Or, mi# n’a pas exactement la même hauteur que le fa voisin, bien que l’intervalle mi–fa soit d’un demi-ton. L’intervalle entre mi# et fa est appelé un comma.
1. Par quel coefficient faut-il multiplier la fréquence de mi# pour obtenir celle du fa voisin ?
Différents « systèmes » ont tenté de corriger ce décalage. On peut citer celui imaginé par Félix Savart, médecin et physicien français, qui a donné son nom à une unité de mesure des intervalles musicaux basée sur le logarithme décimal. L’intervalle en savarts de deux fréquences est égal à mille fois le logarithme décimal des rapports de ces fréquences.
 Buste de Félix Savart (1791–1841)
Buste de Félix Savart (1791–1841)
à l’Institut de France.
2. Sachant que lorsqu’une note est à l’octave d’une autre sa fréquence est double, combien de savarts vaut l’intervalle d’une octave ?
Dans les instruments de musique « modernes », les demi-tons sont de « vrais » demi-tons, c’est-à-dire que la gamme est constituée de douze demi-tons rigoureusement équivalents (un ton de do à ré, un ton de ré à mi, un demi-ton de mi à fa, un ton de fa à sol, un ton de sol à si, un demi-ton de si à do). Lorsque l’octave est ainsi divisée en intervalles chromatiques égaux, on dit que la gamme associée est tempérée.

