Au-delà de l'algèbre
La notion de groupe, de par sa nature structurante, est centrale en algèbre. Mais elle est aussi indispensable en géométrie, où elle permet de comprendre, de classer, de relier, d’étudier les transformations, voire de caractériser différentes géométries. Ainsi, si les symétries n’expliquent pas tout, elles sont souvent présentes, quelquefois de manière invisible.
Mais le concept de groupe ne s’arrête pas là : il a investi d’autres domaines comme l’analyse infinitésimale et la physique mathématique, où les groupes de Lie ont une importance cruciale.
Mais le concept de groupe ne s’arrête pas là : il a investi d’autres domaines comme l’analyse infinitésimale et la physique mathématique, où les groupes de Lie ont une importance cruciale.

LES ARTICLES
Des symétries qui laissent les objets invariants
Élisabeth Busser
En géométrie, quoi de plus naturel de rechercher pour tout objet les transformations qui le laissent inchangé ? Ce faisant, on doit décortiquer ces transformations, identifier les symétries de l'objet, et ô surprise, on trouve tout naturellement des groupes...
Des transformations géométriques en groupes
Gilles Cohen
Abstraite et purement algébrique, la notion de groupe ? Pas du tout! En géométrie, elle permet de ne pas se laisser submerger par la profusion et la diversité apparentes des transformations, ou encore d'appréhender les différents types de symétrie que l'on peut rencontrer.
Le groupe de Klein et ses avatars
Robert Ferréol
Quand on commence à manipuler les groupes, on dresse patiemment la table de ceux qui comportent peu d'éléments. Le groupe à un élément est réduit à l'élément neutre, donc est unique. De même, ceux à deux et trois éléments sont déterminés sans ambiguïté. Les surprises commencent avec quatre éléments...
Le programme d'Erlangen
Hervé Lehning
À l'occasion de sa nomination comme professeur à l'université d'Erlangen, en 1872, Felix Klein, âgé de 23 ans seulement, présenta un programme de recherche en géométrie connu depuis sous le nom de « Programme d'Erlangen ». Au cœur de ce programme figure la notion de groupe.
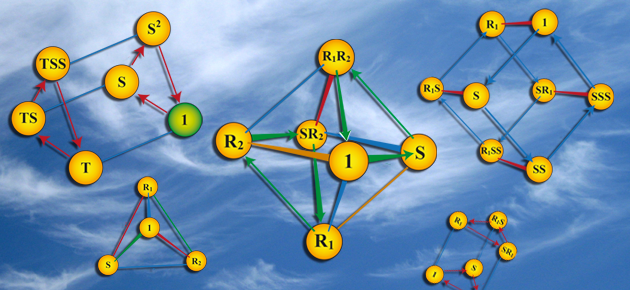
Le diagramme de Cayley
Jean-Jacques Dupas
Comment saisir la structure d'un groupe fini d'un seul coup d'œil ? C'est à cette question que permet de répondre le diagramme de Cayley !
En bref : Les groupes de Lie
Daniel LignonLes groupes introduits par le mathématicien Sophus Lie sont devenus des outils incontournables en physique théorique.