
Géométrie et minéralogie
 Hiroko observe attentivement les végétaux, tel le romanesco, consulte des planches de grains, des coquillages et s'émerveille de leurs torsades, de la beauté de leurs formes. Elle nourrit le projet de devenir sculptrice. Tout en poursuivant ses études de psychologie, elle suit des cours du soir de joaillerie et de français à l'Athénée français de Tokyo.
Hiroko observe attentivement les végétaux, tel le romanesco, consulte des planches de grains, des coquillages et s'émerveille de leurs torsades, de la beauté de leurs formes. Elle nourrit le projet de devenir sculptrice. Tout en poursuivant ses études de psychologie, elle suit des cours du soir de joaillerie et de français à l'Athénée français de Tokyo.
Ses diplômes en poche, Hiroko Miura s'envole pour la France. Elle se spécialise en bijouterie-joaillerie. Installée dans son atelier parisien, elle reste fascinée par le monde des pierres précieuses, et par la géométrie, qu'elle découvre dans la gemmologie et la minéralogie ! Elle crée alors des bijoux architecturaux, notamment des bagues, en métaux précieux.
Une surface minimale : la caténoïde
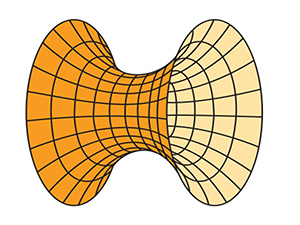 Une représentation paramétrique de la caténoïde est donnée par (x = a ch (u) cos (v), y = a ch (u) sin (v), z = a × u). Cette surface de révolution peut être obtenue par une chaînette tournant autour d'un axe, ou illustrée par l'expérience de deux cercles parallèles, centrés sur le même axe et plongés dans une eau savonneuse. En 1744, Leonhard Euler a prouvé que cette surface est minimale. Un siècle plus tard, le physicien Joseph Plateau lui donne le nom de caténoïde.
Une représentation paramétrique de la caténoïde est donnée par (x = a ch (u) cos (v), y = a ch (u) sin (v), z = a × u). Cette surface de révolution peut être obtenue par une chaînette tournant autour d'un axe, ou illustrée par l'expérience de deux cercles parallèles, centrés sur le même axe et plongés dans une eau savonneuse. En 1744, Leonhard Euler a prouvé que cette surface est minimale. Un siècle plus tard, le physicien Joseph Plateau lui donne le nom de caténoïde.
Topologie et surfaces minimales
Comment l'artiste expérimente-t-elle pour déterminer la forme, le volume et les courbes épurées de la bague Ovni ? Elle plonge deux contours de fil de fer dans une eau savonneuse, puis les oriente de diverses façons en réalisant des déformations topologiques. Le film de savon ainsi construit se comportera comme une membrane qui tendra à réduire sa surface, du fait des forces de tensions superficielles. Lorsque l'état d'équilibre est atteint, la surface est minimale. Décrire les équations d'une telle surface n'est pas facile. Il est possible de faire apparaître plusieurs surfaces minimales stables associées à un même contour.
.jpg)
 Avec une configuration spatiale qui semble intimement liée à celle d'un cube, la bague Quatre Faces de Hiroko Miura présente des courbes architecturées épurées et dynamiques.
Avec une configuration spatiale qui semble intimement liée à celle d'un cube, la bague Quatre Faces de Hiroko Miura présente des courbes architecturées épurées et dynamiques.
