La résolution des équations algébriques
À l’époque où Galois commence à s’intéresser aux mathématiques, les polynômes sont étudiés de longue date et les substitutions et groupes de permutation ont déjà été introduits par Lagrange et étudiés par Cauchy. Ruffini et Abel ont auparavant prouvé qu’il n’est pas possible en général de résoudre de manière algébrique les équations polynomiales de degré 5 ou plus.
Dès lors, quel est l’apport de Galois ? Au-delà de résoudre un problème, il a ouvert un nouveau champ des mathématiques en montrant à quel point un groupe pouvait encoder les propriétés fondamentales d’un polynôme.
Dès lors, quel est l’apport de Galois ? Au-delà de résoudre un problème, il a ouvert un nouveau champ des mathématiques en montrant à quel point un groupe pouvait encoder les propriétés fondamentales d’un polynôme.
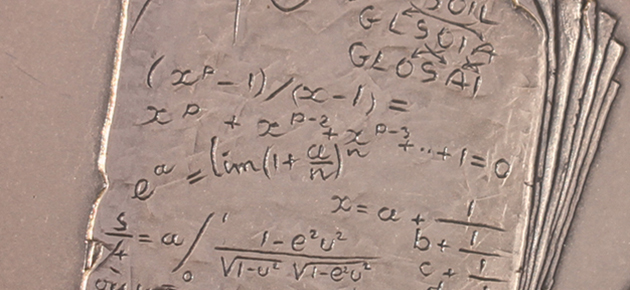
LES ARTICLES
Avant Abel et Galois
Daniel Lignon
Jusqu’à la fin du XVIIIe siècle, l’algèbre s’est résumée à la résolution des équations algébriques. Les pages de cette algèbre-là se sont refermées avec les travaux d’Abel et ceux de Galois. Avant eux, à quelles questions s’intéressait-on ? Quels problèmes pouvait-on espérer résoudre ?
Cauchy, un précurseur oublié
François Lavallou
Ne s’étant pas directement intéressé à la résolution des équations algébriques, Augustin-Louis Cauchy est un oublié de l’histoire de la théorie des groupes. Ses travaux sur les permutations ont pourtant fourni de précieux outils à ceux qui ont travaillé sur la théorie de Galois.
Deux génies et deux approches
pour un même problème
Marc Thierry
Deux méthodes sont connues pour démontrer l’impossibilité de résoudre l’équation algébrique générale de degré 5 : celle donnée par Abel en 1824, précisée en 1826, et celle de Galois en 1829–1830. La théorie de Galois est assez connue alors que les idées d’Abel sont plus rarement exposées.
Au-delà du mémoire de Lagrange
Marc Thierry
Galois a lu à l’adolescence Legendre et Lagrange, et ensuite Gauss et Cauchy. Il cite souvent ces deux derniers, très peu Lagrange. Galois a manifestement été influencé par les idées de son aîné ; il saura cependant aller beaucoup plus loin, profitant de tous les progrès réalisés depuis 1771.
En bref : Histoires de racines
Daniel LignonLes racines de l'unité forment un groupe commutatif. Petits rappels...
En bref : Les ingrédients de base de la théorie de Galois
Bertrand HauchecorneBien qu’inspirée par les travaux de Galois, « sa » théorie s’est développée bien après sa mort et n’a pris son essor qu’avec l’introduction des structures algébriques.
En bref : Le treizième problème de Hilbert
Daniel LignonDavid Hilbert, lors du deuxième congrès des mathématiciens qui s’est tenu à Paris durant l’été 1900, a présenté une liste de questions de recherche importantes pour lui. Celle liste comporte vingt-trois problèmes, issus de tous les domaines : algèbre, géométrie et analyse.








