La vision est suffisamment incongrue pour figer Epsilon sur le chemin qui mène au réfectoire de l'Institut Intergalactique, malgré les gargouillis de son estomac affamé : à genoux sur le sol, à côté d'un mur en construction, Bêta empile des briques en tirant une langue appliquée.
« Mais qu'est-ce que tu fabriques ? Tu as décidé de virer maçon ? »
Tout en considérant son ouvrage avec un froncement de sourcils, le garçon répond : « Non. J'essaye de répondre à un défi du professeur Phi. Je dois trouver quel surplomb maximum on peut atteindre en empilant des briques parfaitement identiques et en les décalant entre elles. »
Epsilon se gratte la tête : « Je doute que Phi s'attende à ce que tu lui bâtisses une tour pour résoudre son problème… On va essayer autrement. »
La jeune fille s'installe à côté de son camarade, dégaine sa tablette et commence à dessiner : « Pour superposer deux briques sans que celle du haut ne bascule, il faut que le centre de gravité de la brique supérieure soit à la verticale d'un point de la brique inférieure. »
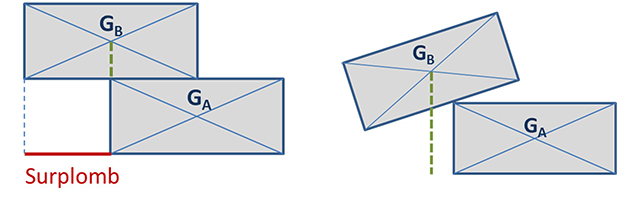
Elle continue à raisonner à voix haute : « Avec deux briques, le surplomb maximum est obtenu en plaçant le centre de gravité de la brique du haut juste au-dessus de l'arête de la brique du bas. »
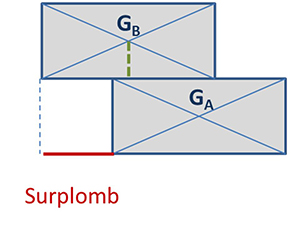« Le souci, fait remarquer Bêta, c'est que l'on ne peut plus poser de brique au-dessus tout en augmentant le surplomb : tout s'écroule, sinon !
– Et si on prenait le problème dans l'autre sens, en regardant comment insérer une nouvelle brique sous les deux premières, tout en assurant l'équilibre ? propose Epsilon. Pour que ça fonctionne, il faut que le centre de gravité du premier bloc soit à la verticale d'un point de la nouvelle brique. Le centre de gravité des deux briques n'est pas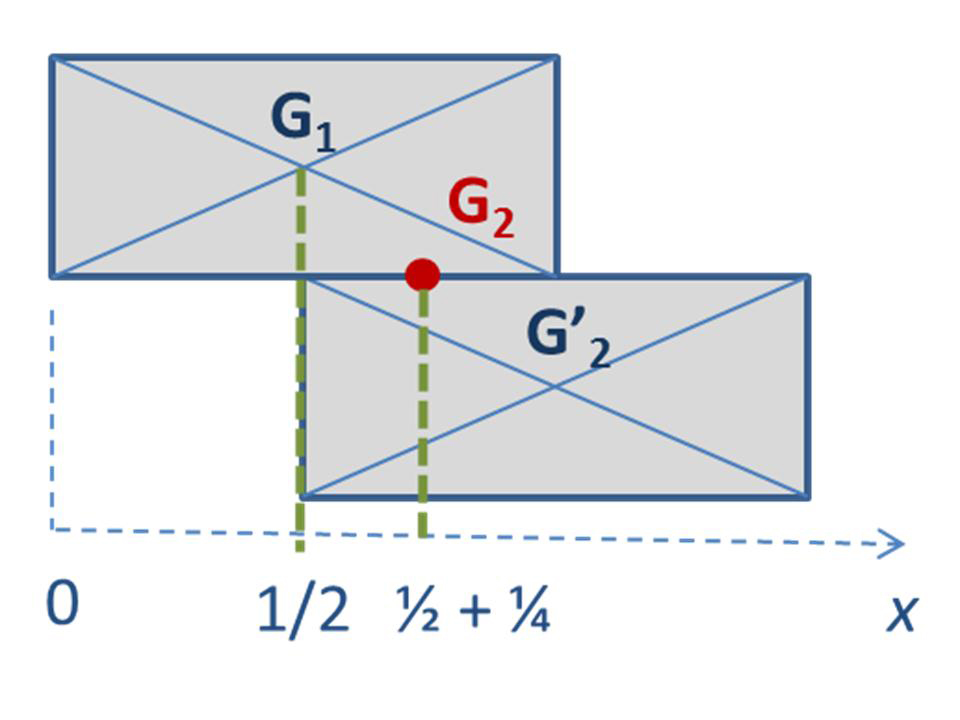 
très compliqué à trouver, en prenant comme unité la longueur d'une brique. »
Et de conclure, triomphante : « Il suffit de placer la nouvelle brique ainsi pour augmenter notre surplomb ! »
« Compris, dit Bêta, le nouveau surplomb est maintenant de ½ + ¼. Mais je crois entendre dans mon oreille la voix du professeur Phi me demandant de “généraliser”… Est-ce qu'on saurait calculer le surplomb obtenu en utilisant n briques ? »
Cher lecteur, pouvez-vous aider Bêta à établir un tel résultat ?
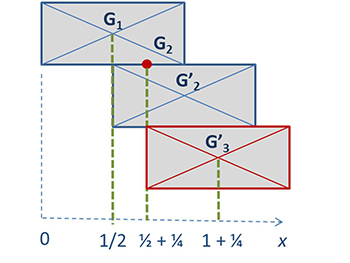
« C'est intéressant, commente Epsilon, une fois posée l'équation, on peut en déduire la réponse au défi du Professeur Phi concernant la longueur maximale du surplomb… »
Et vous, avez-vous cette réponse ?